Задачи Выпуклый анализ (примеры)
Задачи Выпуклый анализ (примеры)
Пример 1. Доказать выпуклость множества 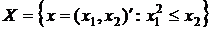 .
.
Пусть 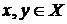 , т. е.
, т. е. 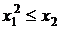 ,
, 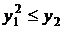 . Тогда для любого
. Тогда для любого 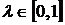 имеем
имеем
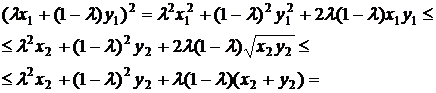
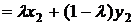 . Следовательно,
. Следовательно, 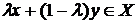 ,
,  , т. е. множество X выпукло.
, т. е. множество X выпукло.
Пример 2. Найти минимальное число A, при котором множество 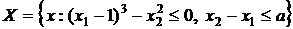 выпукло.
выпукло.
Как видно из рис. , при A= -31/27 множество X будет выпукло.
Пример 3. Доказать, что множество 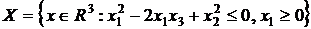 является выпуклым конусом. Изобразить этот конус.
является выпуклым конусом. Изобразить этот конус.
Очевидно, что множество X — конус. Докажем, что X выпуклый конус. Действительно, для любых 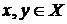 имеем (неравенство Коши-Буняковского и неравенство между средним арифметическим и средним геометрическим).
имеем (неравенство Коши-Буняковского и неравенство между средним арифметическим и средним геометрическим).
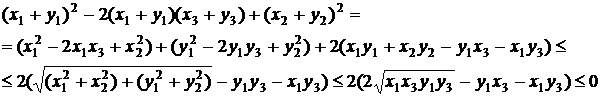
Т. е. 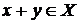 . Таким образом, X — выпуклый конус.
. Таким образом, X — выпуклый конус.
Сечением конуса плоскостью  является круг
является круг 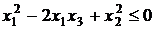 . Если
. Если 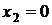 , то получаем конус
, то получаем конус 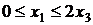 .
.
Пример 4. Записать уравнение гиперплоскости, отделяющей точку 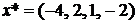 от множества
от множества 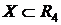 , которое задается системой уравнений
, которое задается системой уравнений

Очевидно, что среди неравенств, задающих множество X, третье неравенство в точке 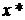 не выполняется. Поэтому в качестве разделяющей (не строго) гиперплоскости можно взять гиперплоскость
не выполняется. Поэтому в качестве разделяющей (не строго) гиперплоскости можно взять гиперплоскость 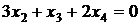 .
.
Пример 5. Записать уравнение гиперплоскости, опорной к множеству
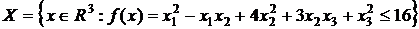
В точке 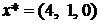 .
.
Функция 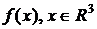 является строго выпуклой, т. к. матрица вторых производных
является строго выпуклой, т. к. матрица вторых производных  , а, значит, множество X выпукло. Тогда опорной гиперплоскостью к множеству X в точке
, а, значит, множество X выпукло. Тогда опорной гиперплоскостью к множеству X в точке 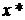 Является, очевидно, касательная плоскость к границе
Является, очевидно, касательная плоскость к границе 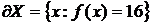 множества X в точке
множества X в точке 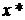 , т. е.
, т. е. 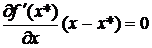 . Имеем
. Имеем 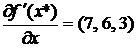 и
и 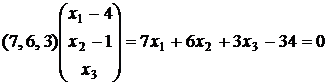 .
.
Пример 6. Записать уравнение гиперплоскости, разделяющей выпуклые множества 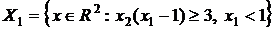 ,
, 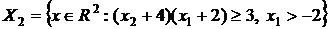 .
.
Ясно, что множества 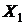 и
и 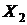 пересекаются (касаются) в единственной точке
пересекаются (касаются) в единственной точке 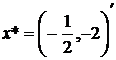 . Поэтому разделяющей гиперплоскостью будет касательная прямая к графику функции
. Поэтому разделяющей гиперплоскостью будет касательная прямая к графику функции 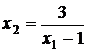 в точке
в точке 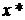 , т. е. прямая
, т. е. прямая 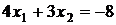 .
.