УПРАЖНЕНИЯ И ЗАДАНИЯ Выпуклое программирование
УПРАЖНЕНИЯ И ЗАДАНИЯ Выпуклое программирование
2.1. Рассмотрим задачу: 
, где 
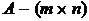— матрица, 
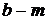— вектор.
A). Привести геометрическую интерпретацию задачи.
B). Записать необходимые условия оптимальности. Являются ли они достаточными.
C). Является ли оптимальный план единственным? Почему?
D). Решить задачу при
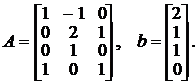
2.2. Рассмотрим задачу: 
, 
. Пусть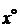 
— локальный оптимальный план и 
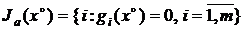, функция 
, 
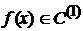, функции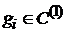 
, 
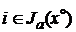, и вогнуты, а функции 
, 
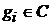. Доказать, что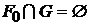 
, где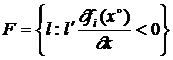 
, 
.
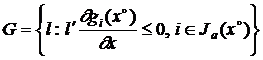2.3. Рассмотрим задачу одномерной минимизации: 
, 
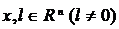— заданные векторы.
A). Записать необходимое условие минимума, если 
. Является ли оно достаточным?
B). Какие предположения о функции F нужно сделать, чтобы необходимое условие стало и достаточным?
2.4. Рассмотрим задачу: 
, 
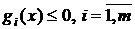. Пусть 
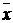— некоторый план задачи, функция , функции ,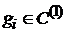 
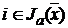, и выпуклы, а при 
непрерывны. Пусть 
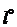— оптимальный план задачи:
A). Показать, что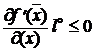 
.
B). Показать, что если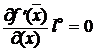 
, то план 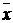удовлетворяет условиям Куна-Таккера.
2.5. Рассмотрим задачу: , 
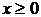, где и выпукла. Показать, что 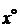— оптимальный план задачи тогда и только тогда, когда L=0, где
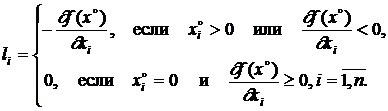
2.6. Рассмотрим задачу: 
, 
, 
, 
.
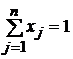Пусть 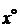— оптимальный план задачи. Показать, что существует такое число K, что 
и 
при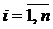 
.
2.7. Рассмотрим задачу: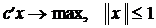 
, где 
.
A). Показать, что =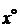
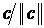удовлетворяет условиям Куна-Таккера и 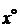— единственный глобальный оптимальный план.
B). Показать (используя а).), что направлением наискорейшего подъема (возрастания) функции F в точке X 
является вектор 
.
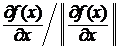2.8. Доказать неравенство
При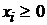 
, 
,
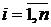Используя условие Куна-Таккера.
2.9. Установить связь между условиями Куна-Таккера для следующих задач
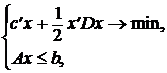и 
Где 
, 
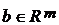, A — матрица размера 
, D — матрица размера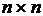 
, D¢=D, 
, 
, 
.
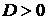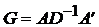2.10. Установить связь между оптимальными планами и условиями Куна-Таккера двух следующих задач:
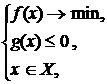
2.11. Рассмотрим задачу
Где , , 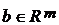A — матрица размера , D — матрица размера 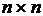, D¢=D.
A). Выписать необходимые условия оптимальности второго порядка.
B). Обязательно ли каждый локальный оптимальный план будет глобальным? Доказать или привести контрпример.
C). Привести необходимые условия оптимальности первого и второго порядков, когда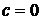 
и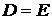 
.
2.12. Записать задачу двойственную к задаче
Где F,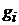 
, 
, 
, 
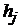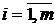, — выпуклые функции, Q — выпуклое множество.
2.13. Рассмотрим задачу
Записать условия Куна-Таккера и убедиться, что они выполняются в точке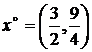 
. Дать геометрическую интерпретацию, показать, что 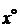— глобальный оптимальный план.
2.14. Решить задачу
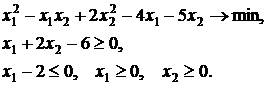
Геометрически; записать условия Куна-Таккера и найти оптимальный план; из точки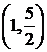 
построить направление спуска.
2.15. Рассмотрим задачу
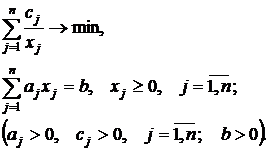
Найти вектор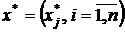 
, удовлетворяющий условиям Куна-Таккера.
2.16. Из функций а) и ограничений б), приведенных ниже, сформировать задачи выпуклого программирования и решить их.
а) целевые функции:
1. 
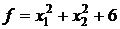
2. 
3. 
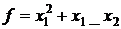
4. 
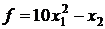
5. 
6. 
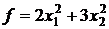
7. 
8. 
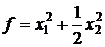
9. 
10. 
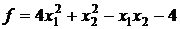
11. 
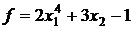
12. 
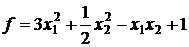
13. 
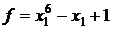
14. 
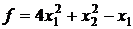
15. 
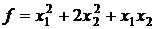
16. 
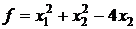
17. 
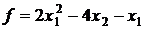
18. 
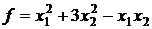
19. 
20. 
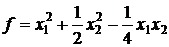
21. 
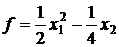
22. 
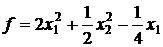
23. 
24. 
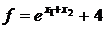
25. 
26. 
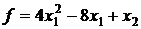
27. 
28. 
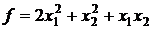
29. 
30. 
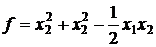
31. 
32. 
33. 
34. 
35. 
36. 
37. 
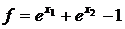
38. 
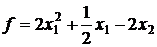
39. 
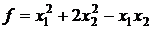
40. 
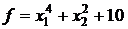
б) ограничения:
|
1. 
|
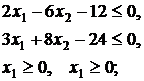
2. 
|
|
3. 
|
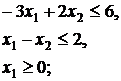
4. 
|
|
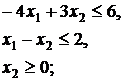
5. 
|
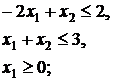
6. 
|
|
7. 
|
8. 
|
|
9. 
|
10. 
|
|
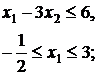
11. 
|
12.
|
|
13. 
|
14. 
|
|
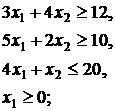
15. 
|
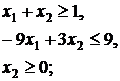
16. 
|
|
17. 
|
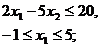
18. 
|
|
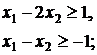
19. 
|
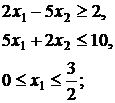
20. 
|
|
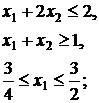
21. 
|
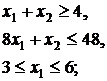
22. 
|
|
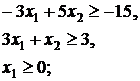
23. 
|
24. 
|
|
25. 
|
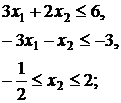
26. 
|
|
27. 
|
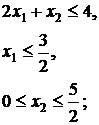
28. 
|
|
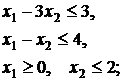
29. 
|
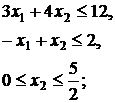
30. 
|
|
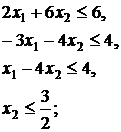
31. 
|
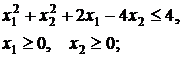
32. 
|
|
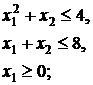
33. 
|
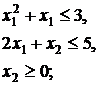
34. 
|
|
35. 
|
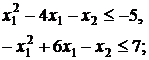
36. 
|
|
37. 
|
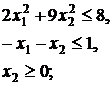
38. 
|
|
39. 
|
40. 
|
|
41. 
|
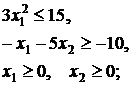
42. 
|
|
43. 
|
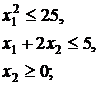
44. 
|
|
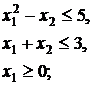
45. 
|
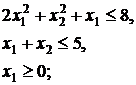
46. 
|
|
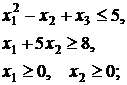
47. 
|
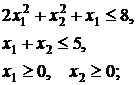
48. 
|
|
49. 
|
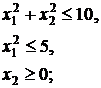
50. 
|
|
51. 
|
52. 
|
|
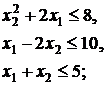
53. 
|
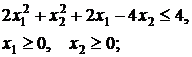
54. 
|
|
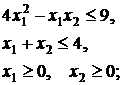
55. 
|
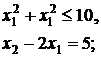
56. 
|
|
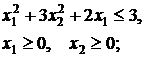
57. 
|
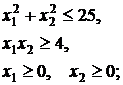
58. 
|
|
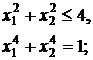
59. 
|
60. 
|
