МЕТОДИЧНІ ВКАЗІВКИ З ВИКОНАННЯ КУРСОВОЇ ТА ДИПЛОМНОЇ РОБІТ

Розподіл Пуасона - граничний випадок біноміального розподілу (рис. 8). За цим законом розподіляється багато випадкових подій, з якими доводиться зустрічатись у мікробіології, радіобіології та й в інших розділах сучасної біології та екології.

Розподіл Максвела використовується для апроксимації емпіричних частот варіаційного ряду, який складається з додатніх чисел і має помірну асиметрію. Крива частот цього типу зручна тим, що будується через рівняння, яке визначається лише одним параметром. Вона досить гнучка і може застосовуватись для вирівнювання асиметричних розподілів різних біологічних ознак, величини яких змінюються за неперервним рядом (рис. 9).

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 x

Рис. 8. Емпіричні (1) та теоретичні (2) частоти (/) розподілу Пуасона

Вказівкою на те, що емпіричний розподіл відповідає законові Максвела, є рівність між середнім квадратичним відхиленням і величиною 0,674а, тобто 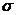= 0,674а, тоді як для розподілу Пуасона характерна рівність 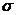2=, а = 0,6267 . Розподіл Максвела може бути репрезентований формулою:

У цій формулі, як уже було вказано вище, А — параметр, який визначається через середнє значення ознаки; , де хі- числові значення випадкової величини X; dх - різниця між двома суміжними значеннями змінної величини X.

Критерій (хі-квадрат). У розділі 1.4.4.1 було розглянуто метод порівняння вибірок за так званими параметричними критеріями – середніми арифметичними виборок та її похибками. Зараз же ознайомимося з критерієм «хі-квадрат» (), який часто ще називають «критерієм відповідності» або «критерієм злагоди» Пірсона. За допомогою зазначеного критерію можливо, з тим або іншим ступенем ймовірності, приймати рішення щодо відповідності емпірично одержаних даних теоретично очікуваним.

Г. М. Зайцев (1984) наводить 9 варіантів застосування цього критерію в біологічних дослідженнях, які, однак, не вичерпують усіх випадків використання критерію у біометрії:

1. Оцінювання співпадіння теоретичних і емпіричних частот зважених рядів.

2. Порівняння дисперсій генеральної сукупності та вибірки.

3. Порівняння двох емпіричних зважених рядів рівного об'єму.

4. Порівняння двох емпіричних зважених рядів різного об'єму.

5. Застосування критерію «хі-квадрат» при вивченні розщеплення гібридів.

6. Застосування критерію «хі-квадрат» у випадку чотирьохпольної таблиці варіант.

Рис. 9. Розподіл Максвела: 1 - емпіричні значення; 2 - теоретична крива; f — частоти

7. Порівняння кількох сукупностей даних.

8. Оцінювання «критерію злагоди» без таблиць.

9. Як критерій гомогенності Брандта-Снедекора.

Лише зрідка трапляється, що емпіричний розподіл цілком відповідає нормальному. Для практичних і наукових робіт буває необхідним встановити, значно чи не дуже розходяться емпіричний та теоретичний ряди. Необхідно встановити таку межу, недосягнення якої (означатиме, що розходження між теоретичним і емпіричним розподілами ще не настільки велике, щоб на нього зважувати, і що даний емпіричний ряд ще можна практично вважати за нормальний.

Критерій був запропонований Пірсоном і визначається за формулою:

,

Де f - емпірична частота; ft - теоретична частота.

Якщо крайні класи розподілу мають теоретичні частоти менші від 1, то при обчисленні їх необхідно об'єднати в один клас разом з найближчим класом, який має частоти ft > 1. Разом із теоретичними треба об'єднати і відповідні фактичні частоти. При підрахунку числа класів об'єднані класи на кожному кінці розподілу треба рахувати за один клас.

Після того, як значення встановлено, треба зважити, значне чи незначне воно для даного розподілу. Для цього використовують Табл. 4 з Додатку 3.

Для того, щоб скористатись цією таблицею, треба попередньо встановити число степенів свободи для розподілу, що аналізується. За умови, що теоретичний розподіл вважається нормальним, всі деталі якого визначаються двома постійними величинами 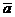та 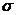, Число степенів свободи в такому випадку дорівнює кількості класів без двох. Наприклад, якщо виділено 9 класів, то число степенів свободи для цього розподілу дорівнюватиме 9-2=7. За число класів береться те, яке залишилось після об'єднання класів з невеликими теоретичними частотами. Для кожного числа степенів свободи в табл. 4 вказано три цифри. Це три граничні значення , що відповідають трьом стандартним ступеням ймовірності (Р3 - 0,999, Р2 =0,99, P1=0,95) того, що розподіли, які показали такі значення ^З2 чи більші, відрізняються вірогідно. Під вірогідною різницею розуміється таке розходження розподілів, яке не може статися внаслідок звичайних випадкових відхилень фактичних частот від теоретичних, чи виборочних частот від генеральних.