Расчетно-графическая работа По дисциплине «Теория случайных процессов» Вариант 23
Факультет экономики и менеджмента
Кафедра экономической
Кибернетики
Расчетно-графическая работа По дисциплине «Теория случайных процессов» Вариант 23.
.
Задание.
Для изучения надежности работы банкомата рассмотрим модель, в которой учитываются три возможных состояния:
S1 – счетчик исправен, но не находится в состоянии эксплуатации,
S2 – счетчик исправен и находится в состоянии эксплуатации,
S3 – счетчик не находится в состоянии эксплуатации по причине неисправности.
Плотности вероятности перехода практически не зависят от времени. Требуется составить систему дифференциальных уравнений Колмогорова и решить задачу Коши, найти вероятности состояния банкомата в момент времени t = 1, если в начальный момент времени t = 0, он находился в состоянии S2, матрица плотностей вероятностей перехода задана:
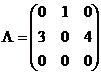
Решение.
1. Изобразим граф состояний системы:

В начальный момент времени t = 0 вектор начального распределения вероятностей имеет следующий вид:
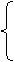
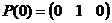 или
или 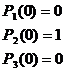
2. Составим систему дифференциальных уравнений Колмогорова:
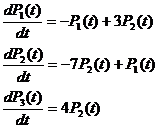
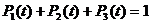
Т. к. ни в одном из трех уравнений системы не присутствует 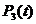 , то для решения системы достаточно будет использовать два уравнения:
, то для решения системы достаточно будет использовать два уравнения:
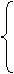
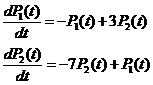
3. Произведем замену и подставим новые переменные в уравнение:
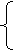
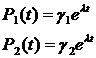
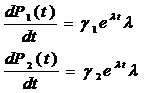
Система примет вид:
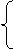
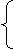
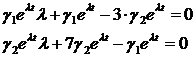
Делим оба уравнения системы на элемент 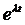 (
(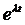 > 0). Получаем:
> 0). Получаем:
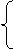
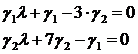
Группируем элементы уравнений:
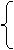
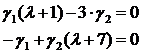
Составим определитель матрицы коэффициентов при неизвестных значениях 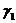 и
и 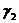
Определитель матрицы равен нулю.
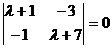
Получаем:
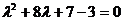
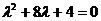
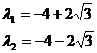
Найденные значения 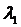 и
и 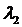 подставляем в систему уравнений (1.6).
подставляем в систему уравнений (1.6).
А). При подстановке 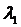 :
:
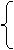
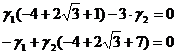
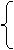
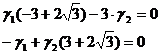
Выразим 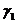 через
через 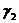 И
И 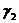 через
через 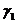 :
:
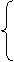
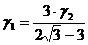 ,
, 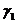 = 1
= 1
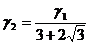 ,
, 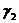 =
= 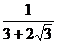
Итог: 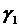 = 1,
= 1, 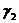 =
= 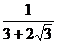 .
.
Б). При подстановке 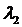 :
:
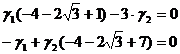
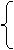
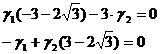
Выразим 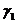 через
через 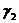 И
И 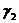 через
через 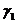 :
:
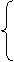
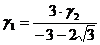 ,
, 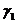 = 1
= 1
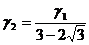 ,
, 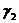 =
= 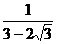
Итог: 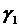 = 1,
= 1, 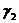 =
= 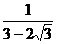 .
.
4. Подставим 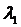 ,
,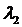 и найденные значения
и найденные значения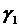 и
и 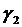 в систему (1.4). Получаем две системы:
в систему (1.4). Получаем две системы:
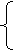
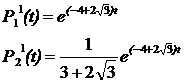
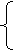
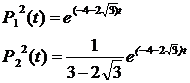
5. Общее решение системы дифференциальных уравнений Колмогорова примет вид:
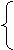
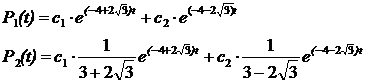
Для решения задачи Коши необходимо задать вектор начального распределения вероятностей. По условию в момент времени t = 0 банкомат находился в состоянии S2.
Вектор начального распределения вероятностей имеет вид:
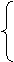
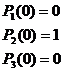
Тогда система уравнений 1.9 примет вид:
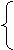
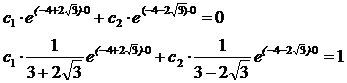
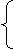
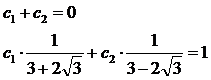
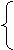
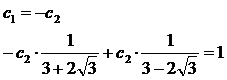
В ходе решения системы уравнений (2.1) получаем следующие значения:
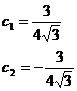
Подставляем найденные значения 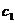 и
и 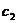 в систему (1.9).
в систему (1.9).
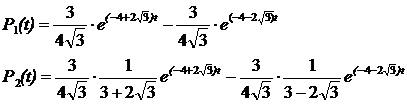
Включим в систему (2.3) уравнение 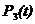 .
. 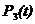 находим из условия (1.2).
находим из условия (1.2).
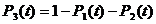
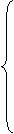
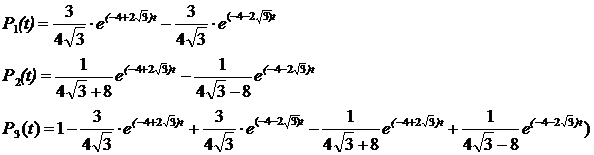
В момент времени t = 1 вероятности состояний примут такие значения:
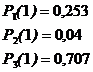
Вывод. Наиболее вероятным состоянием банкомата в момент времени t = 1 будет состояние S3, т. е. счетчик не находится в состоянии эксплуатации по причине неисправности.