УПРАЖНЕНИЯ И ЗАДАНИЯ Выпуклый анализ
УПРАЖНЕНИЯ И ЗАДАНИЯ Выпуклый анализ
1.1. Пусть  ,
, 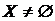 . Показать, что для выпуклости X необходимо и достаточно, чтобы для любого
. Показать, что для выпуклости X необходимо и достаточно, чтобы для любого  из того, что точки
из того, что точки  принадлежат X, следовало, что
принадлежат X, следовало, что  , если
, если  и
и  .
.
1.2. Пусть  — выпуклое множество, A — матрица размера
— выпуклое множество, A — матрица размера  ,
,  . Показать, что следующие множества выпуклы:
. Показать, что следующие множества выпуклы:
а)  .
.
б)  .
.
1.3. Пусть 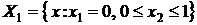 ,
,  . Описать множества
. Описать множества  ,
,  .
.
1.4. Доказать выпуклость следующих множеств в R2: X=

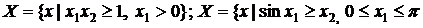 };
};

1.5. Пусть  ,
, 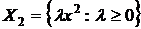 ,
,  . Показать, что
. Показать, что  замкнутое выпуклое множество.
замкнутое выпуклое множество.
1.6. Пусть  и
и 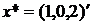 . Найти минимальное расстояние от
. Найти минимальное расстояние от  до X, точку из X, ближайшую к
до X, точку из X, ближайшую к  .
.
1.7. Доказать, что только одна из приведенных ниже систем разрешима:
а) 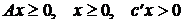 ;
;
б)  .
.
(Указание: использовать теорему Фаркаша).
1.8. Доказать, используя теорему Фаркаша, что только одна из приведенных ниже систем разрешима:
а)  ;
;
б) 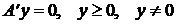 (A —
(A —  — матрица).
— матрица).
1.9. Показать, что приведенные ниже системы имеют решения  и
и  , для которых
, для которых  :
:
а)  ;
;
б) 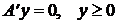 (A —
(A —  — матрица).
— матрица).
1.10. Показать, что разрешима только одна из следующих систем:
а)  ;
;
б) 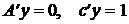 (A —
(A —  — матрица).
— матрица).
1.11. Показать, что если система а) не имеет решения, то система б) разрешима:
а)  ,
,  ,
,  ;
;
б) 
(A — ( ) — матрица, A —
) — матрица, A —  — матрица).
— матрица).
1.12. Пусть  и
и  - выпуклые множества в
- выпуклые множества в  . Показать, что гиперплоскость, строго разделяющая
. Показать, что гиперплоскость, строго разделяющая  и
и  , существует тогда и только тогда, когда
, существует тогда и только тогда, когда

1.13. Рассмотрим множество  . Представить X в виде пересечения полупространств. Выписать эти полупространства в явном виде.
. Представить X в виде пересечения полупространств. Выписать эти полупространства в явном виде.
1.14. Пусть X — непустое множество в  . Показать, что X тогда и только тогда является выпуклым конусом, когда из того, что
. Показать, что X тогда и только тогда является выпуклым конусом, когда из того, что  , следует, что
, следует, что 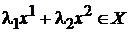 для
для  .
.
1.15. Пусть X — непустое множество в  и
и  . Рассмотрим множество
. Рассмотрим множество 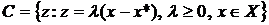 .
.
а) показать, что C — конус и проинтерпретировать это геометрически;
б) показать, что если X — выпуклое множество, то C также выпукло;
с) пусть X — замкнутое множество. Обязательно ли замкнуто C?
1.16. Пусть конус  , где
, где  есть E — окрестность точки X*. Обозначим через K пересечение всех таких конусов, т. е.
есть E — окрестность точки X*. Обозначим через K пересечение всех таких конусов, т. е.  . Нарисовать конус K. (Это множество K называется конусом касательных к множеству X в точке X*).
. Нарисовать конус K. (Это множество K называется конусом касательных к множеству X в точке X*).
1.17. Найти минимальное значение параметра С, при котором множество  выпукло:
выпукло:
|
№№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
A
|
2
|
1
|
4
|
5
|
3
|
1
|
5
|
3
|
4
|
2
|
|
B
|

|
5
|

|

|

|
6
|
4
|
8
|
3
|
1
|
|
№№
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
A
|
2
|
1
|
3
|
5
|
4
|
4
|
5
|
1
|
2
|
3
|
|
B
|

|
9
|
10
|
11
|
4
|
3
|
5
|
7
|
10
|
6
|
1.18. Доказать, что множество  является выпуклым конусом и изобразить его на плоскости:
является выпуклым конусом и изобразить его на плоскости:
№№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
A
|
2
|
3
|
2
|
2
|
4
|
4
|
5
|
5
|
3
|
3
|
|
B
|
-7
|
4
|
-5
|
-5
|
-15
|
-11
|
-13
|
-17
|
-1
|
-8
|
|
С
|
6
|
-4
|
2
|
-3
|
9
|
-6
|
6
|
6
|
-4
|
4
|
|
№№
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
A
|
2
|
3
|
3
|
5
|
5
|
6
|
2
|
2
|
6
|
4
|
|
B
|
-
|
-
|
-
|
-
|
-2
|
-1
|
7
|
-3
|
1
|
-5
|
|
C
|
-3
|
-4
|
-2
|
-4
|
-3
|
-5
|
3
|
-5
|
-5
|
-6
|
1.19. Найти минимальное значение параметра A, при котором множество
 выпукло.
выпукло.
1.20. Записать уравнение гиперплоскости, строго отделяющей точку X*=(3,2,1,1)¢ от множества X, которое задается системой

|
№№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
A
|
6
|
3
|
-1
|
1
|
6
|
3
|
3
|
-1
|
7
|
8
|
|
B
|
-1
|
6
|
-1
|
4
|
0
|
0
|
2
|
4
|
1
|
0
|
|
C
|
-1
|
1
|
2
|
-1
|
-1
|
4
|
4
|
0
|
-1
|
1
|
|
№№
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
A
|
2
|
2
|
-3
|
-2
|
7
|
4
|
9
|
4
|
-2
|
8
|
|
B
|
5
|
1
|
6
|
-2
|
-2
|
0
|
1
|
7
|
5
|
2
|
|
C
|
0
|
3
|
-1
|
3
|
1
|
5
|
0
|
-1
|
1
|
1
|
|
№№
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|
A
|
10
|
1
|
7
|
6
|
6
|
3
|
-6
|
9
|
8
|
10
|
|
B
|
-1
|
3
|
-2
|
0
|
4
|
6
|
3
|
4
|
7
|
4
|
|
C
|
-1
|
2
|
-1
|
5
|
8
|
0
|
-1
|
6
|
11
|
8
|
1.21. Записать уравнение гиперплоскости, опорной к множеству  в точке X*=
в точке X*=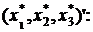
|
№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|

|
-
|
-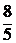
|
0
|

|
0
|
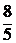
|
0
|

|
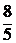
|
0
|
|
|
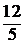
|
0
|

|
0
|
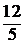
|

|
-
|
-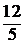
|
0
|
-
|
|
|
0
|
3
|
4
|
4
|
3
|
0
|
4
|
0
|
-3
|
-4
|
|
№№
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|

|
0
|

|
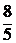
|
0
|
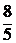
|

|
0
|
-
|
-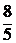
|
0
|
|
|

|
0
|
-
|
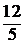
|
0
|
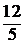
|
-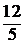
|
0
|
-
|
-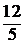
|
|
|
-4
|
-4
|
0
|
-3
|
3
|
0
|
3
|
4
|
0
|
-3
|
|
№№
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|

|

|
-
|
0
|
1
|
-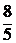
|
-
|
0
|
-
|

|
-
|
|
|
0
|
0
|
2
|

|
0
|
0
|
-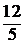
|
-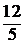
|
0
|
0
|
|
|

|
-
|

|
0
|
-3
|
-4
|
-3
|
0
|

|
-
|
Если точка X*ÏX, то выписать уравнение отделяющей гиперплоскости.
1.22. Выписать уравнение гиперплоскости, опорной к множеству  и отделяющей его от точки X*=
и отделяющей его от точки X*=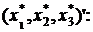
|
№№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|

|

|

|

|

|

|

|

|

|

|
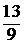
|
|
|

|

|

|

|

|

|

|

|

|

|
|
|

|
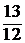
|

|

|

|

|

|

|

|

|
№№
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|

|

|

|
2
|
2
|
4
|

|
3
|
4
|
0
|

|
|
|

|

|
1
|
1
|
3
|
1
|
1
|
0
|
3
|

|
|
|

|

|
1
|
2
|
5
|
1
|
3
|
2
|
5
|

|
|
№№
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|

|

|

|

|

|

|

|

|

|

|

|
|
|

|

|

|

|

|

|

|

|
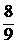
|

|
|
|

|

|
1
|
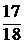
|

|

|

|
1
|
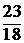
|
1
|
1.23. Записать уравнение гиперплоскости, разделяющей множества  ,
,  , где
, где
|
№№
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
A
|

|
4
|

|
25
|

|
25
|
25
|

|

|
9
|
|
B
|
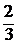
|
1
|
1
|
12
|

|
18
|
9
|
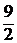
|

|
2
|
|
C
|

|
9
|
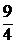
|
3
|

|
2
|
4
|

|
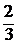
|
8
|
|
№№
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
A
|

|
25
|

|
9
|
25
|

|

|
25
|
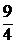
|
1
|
|
B
|

|
2
|
|
8
|
3
|
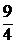
|

|
4
|

|
4
|
|
C
|
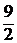
|
18
|

|
2
|
12
|
1
|

|
9
|
5
|
1
|
|
№№
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
|
A
|
5
|
9
|
16
|

|
10
|
7
|
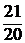
|
1
|

|

|
|
B
|
4
|
1
|
1
|

|
5
|
2
|

|
3
|
1
|
3
|
|
C
|
1
|
3
|
5
|
3
|
2
|
3
|
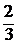
|

|

|

|
1.24. Пусть  и выпукло. Показать, что функция F(X), XÎX, вогнута тогда и только тогда, когда ее подграфик является выпуклым множеством.
и выпукло. Показать, что функция F(X), XÎX, вогнута тогда и только тогда, когда ее подграфик является выпуклым множеством.
1.25. Пусть X — непустое выпуклое множество в  . Показать, что функция F(X), XÎX, выпукла тогда и только тогда, когда для
. Показать, что функция F(X), XÎX, выпукла тогда и только тогда, когда для  и
и  справедливо неравенство
справедливо неравенство
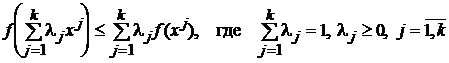 .
.
1.26. Проверить, является ли функция F выпуклой (вогнутой) на заданном множестве X, или указать такие точки из X, в окрестности которых F не является ни выпуклой, ни вогнутой.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
6.  .
.
7. 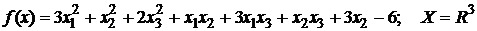 .
.
8.  .
.
9.  .
.
10. 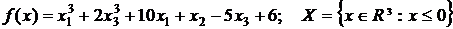 .
.
11.  .
.
12.  .
.
13. 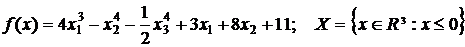 .
.
14.  .
.
15. 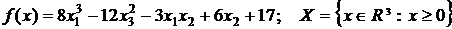 .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20.  .
.
21. 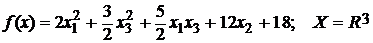 .
.
22.  .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30.  .
.
31. 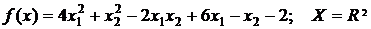 .
.
32.  .
.
33. 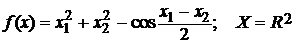 .
.
34.  .
.
35.  .
.
36.  .
.
37.  .
.
38.  .
.
39.  .
.
40.  .
.
41. 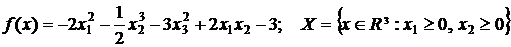 .
.
42.  .
.
43.  .
.
44.  .
.
45.  .
.
46.  .
.
47.  .
.
48.  .
.
49. 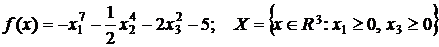 .
.
50.  .
.
51.  .
.
52.  .
.
53. 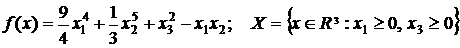 .
.
54.  .
.
1.27. Пусть функция F(X) непрерывна на  и для каждой точки XÎ
и для каждой точки XÎ существует окрестность, в которой F(X) выпукла. Является ли F(X) выпуклой на
существует окрестность, в которой F(X) выпукла. Является ли F(X) выпуклой на  ?
?
1.28. Пусть функция G(X), XÎ , вогнута. Показать, что функция F(X)=1/G(X) выпукла на множестве
, вогнута. Показать, что функция F(X)=1/G(X) выпукла на множестве  .
.
1.29. Пусть  , — выпуклые функции. Показать, что функция
, — выпуклые функции. Показать, что функция  выпукла. Доказать аналогичное утверждение для вогнутых функций.
выпукла. Доказать аналогичное утверждение для вогнутых функций.
1.30. Пусть  , — выпуклые функции. Показать, что функция
, — выпуклые функции. Показать, что функция  , выпукла.
, выпукла.
1.31. Пусть X — непустое выпуклое множество в  и
и  . (Функция F(Y) задает расстояние от точки Y до множества X и называется функцией расстояния). Доказать, что F(Y) — выпуклая функция.
. (Функция F(Y) задает расстояние от точки Y до множества X и называется функцией расстояния). Доказать, что F(Y) — выпуклая функция.
1.32. Пусть  . Выписать в явном виде функцию расстояния от Y до множества X.
. Выписать в явном виде функцию расстояния от Y до множества X.
1.33. Пусть F(X), XÎ , — выпуклая функция. Показать, что функция H(X)=G(F(X)), XÎ
, — выпуклая функция. Показать, что функция H(X)=G(F(X)), XÎ , выпукла, если G — неубывающая выпуклая функция.
, выпукла, если G — неубывающая выпуклая функция.
1.34. Пусть X — непустое ограниченное выпуклое множество в  , F(Y), YÎ
, F(Y), YÎ , — опорная функция множества X, определяемая следующим образом:
, — опорная функция множества X, определяемая следующим образом:
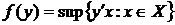 . Доказать, что функция F выпукла. Показать, что если F(Y)=Y¢X*, где X*ÎX, то X* — cубградиент функции F в точке Y.
. Доказать, что функция F выпукла. Показать, что если F(Y)=Y¢X*, где X*ÎX, то X* — cубградиент функции F в точке Y.
1.35. Пусть  , где
, где 
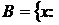
 . Выписать в явном виде опорную функцию, определенную в задаче 34.
. Выписать в явном виде опорную функцию, определенную в задаче 34.
1.36. Функция F(X), XÎ , называется калибровочной, если для всех XÎ
, называется калибровочной, если для всех XÎ и
и  выполняется равенство
выполняется равенство  . Калибровочная функция субаддитивна, если
. Калибровочная функция субаддитивна, если  для любых
для любых  .
.
Доказать, что для калибровочной функции субаддитивность эквивалентна выпуклости.
1.37. Пусть F(X), XÎ , — выпуклая функция. Показать, что X является субградиентом функции F в точке X* тогда и только тогда, когда гиперплоскость
, — выпуклая функция. Показать, что X является субградиентом функции F в точке X* тогда и только тогда, когда гиперплоскость  является опорной к надграфику функции F в точке (X*, F(X*)).
является опорной к надграфику функции F в точке (X*, F(X*)).
1.38. Пусть F — выпуклая на  функция. Показать, что совокупность всех субградиентов функции F в данной точке образует выпуклое замкнутое множество.
функция. Показать, что совокупность всех субградиентов функции F в данной точке образует выпуклое замкнутое множество.
1.39. Рассмотрим функцию F, определенную с помощью следующей задачи:

а) Показать, что функция F вогнута.
б) Вычислить значение F в точке (1,1).
с) Найти совокупность субградиентов функции F в точке (1,1).
1.40. Рассмотрим функцию  . Показать, что если X=0, то X — субградиент функции F(X) в этой точке в том и только том случае, если
. Показать, что если X=0, то X — субградиент функции F(X) в этой точке в том и только том случае, если 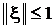 . Если же
. Если же  , то X является субградиентом функции F в точке X тогда и только тогда, когда
, то X является субградиентом функции F в точке X тогда и только тогда, когда  и
и  .
.
1.41. Пусть F1(X), F2(X), XÎ , — дифференцируемые выпуклые функции, F(X)=max{ F1(X), F2(X)}, и X* такая, что F(X*)=F1(X*)=F2(X*). Показать, что вектор X является субградиентом функции F(X) в точке X* тогда и только тогда, когда
, — дифференцируемые выпуклые функции, F(X)=max{ F1(X), F2(X)}, и X* такая, что F(X*)=F1(X*)=F2(X*). Показать, что вектор X является субградиентом функции F(X) в точке X* тогда и только тогда, когда  , где
, где  . Обобщить это утверждение на конечное число функций.
. Обобщить это утверждение на конечное число функций.


 , если
, если  и
и 
 в точке X*=
в точке X*= , где
, где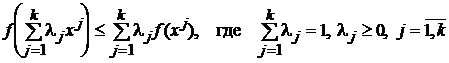 .
. .
. , выпукла.
, выпукла.