Задача авторегрессия и автокорреляция возмущений
Задача авторегрессия и автокорреляция возмущений
АВТОРЕГРЕСССИЯ АВТОКОРРЕЛЯЦИЯ ВОЗМУЩЕНИЙ.
При применении регрессионного анализа на базе временных рядов в классической модели часто обнаруживается нарушение: Возмущения в уравнении являются автокоррелированными.
Существует два альтернативных варианта действий при обнаружении автокорреляции:
• исследователь может попытаться изменить спецификацию модели так, чтобы устранить автокорреляцию возмущений (путем введения дополнительных признаков - регрессоров);
• выбрать такой метод оценки параметров, который при наличии автокорреляции возмущений мог бы по возможности максимально обеспечить требуемые свойства полученных оценок, например Метод Эйткена.
IV. 1. Авторегрессионный процесс первого порядка.
Грубо говоря, Автокорреляция возмущений означает, что 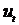 в регрессионном уравнении для периода
в регрессионном уравнении для периода 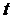 зависит от возмущений более ранних периодов в том же уравнении. В простейшем случае здесь имеет место Авторегрессионный процесс первого порядка.
зависит от возмущений более ранних периодов в том же уравнении. В простейшем случае здесь имеет место Авторегрессионный процесс первого порядка.
Определение: Возмущение 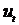 подчиняется авторегрессионному процессу первого порядка, если выполняются следующие условия:
подчиняется авторегрессионному процессу первого порядка, если выполняются следующие условия:
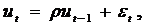 где
где 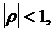
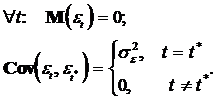 (IV. 1)
(IV. 1)
Замечание:
• Условие стационарности определило требование, согласно которому 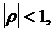 что гарантирует, что влияние запаздывающего возмущения будет тем меньше, чем больше запаздывание. Таким образом, коэффициенты при
что гарантирует, что влияние запаздывающего возмущения будет тем меньше, чем больше запаздывание. Таким образом, коэффициенты при  соответственно
соответственно 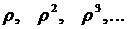
• Случайная переменная 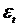 , как специфицировано в формуле (IV. 1), свободна от автокорреляции и для всех
, как специфицировано в формуле (IV. 1), свободна от автокорреляции и для всех 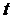 имеет одинаковую дисперсию
имеет одинаковую дисперсию 
• В случае, если условия наличия авторегрессионного процесса первого порядка выдвигаются в качестве альтернативной гипотезы, то отсутствие автокорреляции может быть записано так: 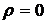 (нулевая гипотеза).
(нулевая гипотеза).
• Авторегрессионные процессы более высокого порядка могут быть выдвинуты в качестве альтернативных гипотез, если в данных имеются циклические колебания (например, сезонные колебания в сельскохозяйственных работах имеется авторегрессия второго порядка, а в квартальных данных может наблюдаться авторегрессия четвертого порядка).
IV. 2. Форма ковариационной матрицы возмущений.
В случае авторегрессии, ковариационная матрица имеет следующий вид:

Здесь 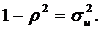
Матрица существенно отличается от диагональной матрицы, типичной для классической модели регрессии.
Для того, чтобы в этом случае можно было бы провести оценку по методу Эйткена, необходима матрица 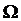 . Все элементы
. Все элементы 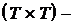 Мерной матрицы
Мерной матрицы 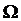 либо известны, либо легко вычисляемы, если известно значение
либо известны, либо легко вычисляемы, если известно значение 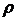 . Однако в эмпирических исследованиях
. Однако в эмпирических исследованиях 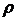 всегда неизвестно и должно быть статистически оценено.
всегда неизвестно и должно быть статистически оценено.
IV. 3. d-Тест Дарбина-Уотсона.
При D-тесте Дарбина-Уотсона нулевой гипотезы предполагается классическая линейная модель нормальной регрессии: регрессоры нестохастичны. Таким образом, запаздывающие значения регрессанда не допускаются в качестве регрессоров.
Как альтернативную гипотезу в более широком смысле D-тест использует условия существования авторегрессионного процесса первого порядка.
D - статистика Дарбина-Уотсона вычисляется по формуле:
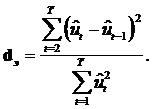 (IV. 2)
(IV. 2)
Точное распределение D-статистики в (IV. 2) зависит от следующих факторов:
•  Длины наблюдаемого ряда;
Длины наблюдаемого ряда;
• 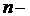 Количества выделенных признаков (регрессоры);
Количества выделенных признаков (регрессоры);
• 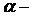 Уровня значимости;
Уровня значимости;
• конкретных числовых значений регрессоров уравнения.
Согласно последнему, при каждом применении D-теста, необходимо заново пересчитывать значения регрессоров. Для преодоления этих трудностей существует таблица D-критерия. Эта таблица содержит необходимые значения  и
и 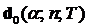 для одностороннего теста и уровня значимости
для одностороннего теста и уровня значимости 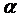 . Здесь
. Здесь 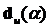 и
и 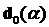 верхняя и нижняя критические границы показателя
верхняя и нижняя критические границы показателя 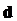 соответственно.
соответственно.
При проведении двустороннего теста для уровня значимости 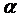 необходимо использовать табличные величины для уровня значимости
необходимо использовать табличные величины для уровня значимости 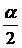 . Следовательно:
. Следовательно: 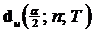 и
и 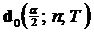 - верхняя и нижняя критические границы соответственно.
- верхняя и нижняя критические границы соответственно.
Для определения областей принятия решений при D-тесте на автокорреляцию возмущений существует правило:
• Если величина D-Статистики приближается к значению 2.0 - автокорреляция возмущений первого порядка отсутствует;
• Чем больше расчетная величина D-Статистики стремится к нулю, тем сильнее проявляются признаки положительной автокорреляции;
• Чем ближе величина D-Статистики к величине 4.0, тем сильнее признаки отрицательной автокорреляции.
Против основной (нулевой) гипотезы 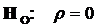 три альтернативные гипотезы.
три альтернативные гипотезы.
0 2 4
|
- область принятия гипотезы 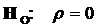 ; ;
|
|
|
|
- область отклонения гипотезы 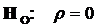 ; ;
|
|
|
|
- инконклюзивная область.
|
К гипотезе I: тест с альтернативной гипотезой 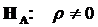 (двусторонний тест, нормальный случай).
(двусторонний тест, нормальный случай).
Отклонение: 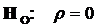 , если
, если 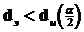 или
или 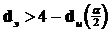 .
.
Принятие: 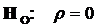 , если
, если 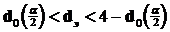 .
.
Неопределенность: Значения 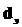 в прочих областях (обозначение - ?)
в прочих областях (обозначение - ?)
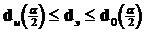 или
или 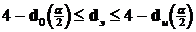 .
.
К гипотезе II: тест с альтернативной гипотезой 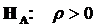 на положительную автокорреляцию (односторонний тест, нормальный случай).
на положительную автокорреляцию (односторонний тест, нормальный случай).
Отклонение: 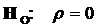 , если
, если 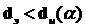 .
.
Принятие: 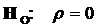 , если
, если 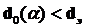 .
.
Неопределенность: Значения 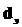 в области
в области 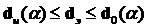 .
.
К гипотезе III: тест с альтернативной гипотезой 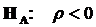 на отрицательную автокорреляцию (односторонний тест, нормальный случай).
на отрицательную автокорреляцию (односторонний тест, нормальный случай).
Отклонение: 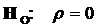 , если
, если 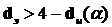 .
.
Принятие: 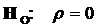 , если
, если 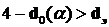 .
.
Неопределенность: Значения 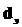 в области
в области 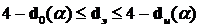 .
.
Инконклюзивная область - область неопределенных решений. При прочих равных условиях она тем больше, чем:
• меньше  Длина ряда наблюдений;
Длина ряда наблюдений;
• больше  Количество выделенных признаков (регрессоров);
Количество выделенных признаков (регрессоров);
• больше  Уровень значимости.
Уровень значимости.
IV. 4. Схема применения D-Теста.
10. Подберите к данной нулевой (основной) гипотезе 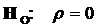 подходящую альтернативную гипотезу:
подходящую альтернативную гипотезу:
I. 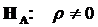
II. 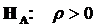
III. 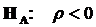
20. Выберите высокий уровень значимости 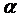 .
.
30. По таблицам найдите верхнее и нижнее значения D-критерия и рассчитайте с ними соответствующие области принятия решений.
40. Рассчитайте величину D-статистики.
50. Примите решение.
60. Интерпретируйте результат теста.