КОНТРОЛЬНАЯ РАБОТА ПО КУРСУ: «ЛЕСНАЯ ТАКСАЦИЯ» 2006
КОНТРОЛЬНАЯ РАБОТА ПО КУРСУ: «ЛЕСНАЯ ТАКСАЦИЯ» 2006
1. Сбег ствола и его влияние на объём бревна.
Диаметр древесного ствола от комля к вершине постепенно уменьшается. Это уменьшение, приходящееся на единицу длины ствола (чаще всего 1М), Называется сбегом. Сбег может быть абсолютным или относительным.
Абсолютный сбег равен разности между диаметрами двух сечений ствола, отстоящих одно от другого на расстоянии 1М. Допустим, что диаметр ствола на расстоянии 1М От комля D1 30См, А на расстоянии 2М От комля D2 29См. Разность между этими двумя диаметрами, равная 1См, И составляет абсолютный сбег на этом участке ствола.
При определении относительного сбега диаметр ствола, измеряемый на высоте груди, принимают за 100. Все прочие диаметры, измеряемые в разных сечениях, выражают в процентах от диаметра на высоте груди. В результате получают процентный ряд, характеризующий относительное изменение диаметра ствола, или относительный сбег. Если диаметр сечения, отстоящего от диаметра на высоте груди на 1М, Равен 96%, относительный сбег составит 4%.
На отдельных участках ствола величина сбега различна: в нижней части из-за корневых наплывов он будет довольно большим, в средней части ствола уменьшается и к вершине снова возрастает.
При оценке различий в сбеге у отдельных бревен принято устанавливать средний сбег. Средний сбег Sср равен разности между диаметрами в нижнем Dн и верхнем dв отрезе, деленной на длину бревна L:
Sср = (Dн - dв) : L
У бревен, заготовленных из комлевой части ствола, на первом метре от комля довольно часто имеются корневые наплывы. При установлении среднего сбега таких бревен разность между диаметром сечения, находящегося на высоте 1М От комля D1 и верхним диаметром dB делят на длину бревна L, Уменьшенную на 1М:
Sср = (D1 – dв) : (L – 1)
При установлении величины среднего сбега образующие боковой поверхности бревен принимают условно за прямую. Между тем известно, что образующая древесных стволов представляет собой сочетание ряда кривых.
При распиловке бревен на доски, а также при использовании их в строительстве учитывают диаметр верхней части бревен, не превышающей по длине 3М. Различия в сбеге в остальной части бревна с производственной точки зрения интереса не представляют. При распиловке бревен на длинные доски, имеющие геометрически правильную форму (параллелепипеды), безразлично, будет ли бревно иметь форму усеченного конуса, где образующей является прямая, или форму параболоида с выпуклой образующей. В обоих случаях периферическая часть бревна окажется в отходах. На участке ствола длиной 3М Разница в диаметрах при конической и параболической форме этих участков не превышает нескольких миллиметров, т. е. находится в пределах точности обмера. Поэтому при использовании древесины в народном хозяйстве определяют лишь среднюю величину сбега.
Вопрос о величине среднего сбега изучался Н. П. Анучиным. Было детально обмерено свыше 4 тыс. бревен и установлено, что величина среднего сбега находится в прямой зависимости от толщины бревен. Зависимость эта характеризуется следующим уравнением:
Sср = 0,39 + 0,021 D
Где D — диаметр, См (для комлевых бревен — на расстоянии 1М От комля, а для всех остальных — в нижнем торце).
Чтобы определить, как изменяется величина сбега у отдельных бревен, были вычислены среднеквадратические отклонения от средних норм.
Наибольшее изменение в сбеге наблюдается у крупных бревен. Это, по-видимому, объясняется тем, что бревна средней толщины заготовляют в большинстве случаев из срединных частей стволов, имеющих более правильную форму.
Среднеквадратические отклонения сбега от средних норм
У бревен разной толщины
|
Толщина бревен
(комлевых — на расстоянии 1М От комля,
Всех остальных —
В нижнем торце), См
|
Средний сбег,
См
|
Среднеквадрати-
Ческое отклонение, См
|
Коэффициент
Вариации, %
|
|
15
|
0,77
|
0,34
|
44,4
|
|
20
|
0,84
|
0,32
|
38,1
|
|
25
|
0,89
|
0,29
|
32,6
|
|
30
|
0,94
|
0,27
|
28,7
|
|
35
|
1,06
|
0,32
|
31,9
|
|
40
|
1,18
|
0.37
|
31,4
|
|
45
|
1,37
|
0,36
|
26,3
|
|
50
|
1,67
|
0,63
|
38,3
|
|
55
|
1,87
|
0,87
|
47,5
|
|
В среднем
|
0,96
|
0,38
|
38,5
|
Среднеквадратические отклонения изменяются от 0,27 до 0,87см. Они составляют округленно от 1/4 до 1/2, а в среднем почти равны 1/3 величины абсолютного сбега. Средний коэффициент вариации равен 38,5%, средний сбег 0,96См На 1М Длины бревна. Следовательно, по закону нормального распределения у 68 бревен из каждых 100 расхождение со средней величиной сбега не будет превышать ±0,38См На 1М Длины бревна, а средний сбег будет 0,59 — 1,33См.
Анализ опытных данных показывает, что сбег сосновых и еловых бревен изменяется примерно в одних и тех же пределах и средние величины его близки между собой. Поэтому для этих пород, могут применяться одни и те же таблицы объемов бревен.
Разделение бревна на цилиндрическую часть и зону сбега
При изучении влияния сбега на объем бревна его делят на две части: боковую, или периферическую, которая называется зоной сбега, и цилиндрическую.
Объем цилиндрической части бревна называется цилиндрической кубатурой. Она определяется как объем цилиндра, основанием которого является верхний торец бревна, а высота равна длине бревна. У бревен, имеющих одинаковые длину и верхние диаметры, независимо от различий в их сбеге цилиндрическая кубатура будет одинаковой. Чем больший сбег имеет бревно, тем больший процент его объема приходится на зону сбега. У бревен средней длины (6М) на зону сбега падает 20,8% объема бревна, у длинных (10м) — 31,1%, т. е. в 1,5 раза больше. У двухметровых бревен объем зоны сбега в 2,4 раза меньше, чем у бревен средней длины.
 В отношении толщины бревен установлена следующая зависимость: чем бревно толще, тем объем зоны сбега (в%) меньше. Так, у шестиметровых бревен при толщине 15См Объем зоны сбега составляет 24,2%, при толщине 25См 19,4%, при толщине 40См 16,7%.
В отношении толщины бревен установлена следующая зависимость: чем бревно толще, тем объем зоны сбега (в%) меньше. Так, у шестиметровых бревен при толщине 15См Объем зоны сбега составляет 24,2%, при толщине 25См 19,4%, при толщине 40См 16,7%.
Сбег у отдельных бревен сильно изменяется. При пользовании таблицами объемов бревен, требующими измерений верхних диаметров и длины бревен, величина этих изменений не учитывается. Следовательно, ошибки в определении объема бревен по таким таблицам объясняются неточным учетом зоны сбега.
Так как на долю зоны сбега у коротких бревен приходится наименьшая часть их объема, неточный учет особенностей их сбега не приводит к существенным ошибкам при определении общего объема бревен. Например, у двухметровых бревен зона сбега, в 2 раза большая средней, дает ошибку при определении по таблицам общего объема бревен лишь на 8,7%. У длинных же бревен всякие отклонения в величине сбега влияют на фактический объем бревен значительно больше.
При средней величине сбега 0,96См И диаметре в верхнем отрезе 20См Срединный диаметр шестиметровых бревен будет равен
20 + 0,96 х 3 ~ 23См.
Изменение сбега характеризуется отклонением ±0,38См. Соответственно этому диаметры шестиметровых бревен средней толщины на половине их длины будут следующими:
23 ± 0,38 х 3 = 23 ± 1,14См.
Следовательно, отклонение от величины срединного диаметра бревна составляет
± (1,14 х 100) : 32 = ± 5%
Ошибка в определении диаметра приводит к удвоенной ошибке в определении площади круга. При учете бревен по диаметрам в верхнем отрезе срединные диаметры этих бревен находят с погрешностью ±5%, которая в свою очередь влечет за собой удвоенную погрешность в определении срединных сечений бревен, т. е. ±10%.
Как уже говорилось, объем бревна можно определить, умножив площадь его срединного сечения на длину. При этом способе относительная ошибка в вычислении срединного сечения вызывает такую же относительную ошибку в определении объема бревна. При средней длине бревен 6М Определение их объемов по таблицам, для пользования которыми необходимо измерять верхние диаметры и длину бревен, сопряжено с ошибками, в среднем равными ±10%. В 68 случаях из 100 ошибка в определении объемов бревен не превышает ±10%, в 27 случаях ±20% и в 5 случаях ±30%.
С увеличением толщины бревен ошибки в объемах уменьшаются, с увеличением длины возрастают, с уменьшением длины падают.
При составлении таблиц объемов обмеряют бревна, имеющие разный сбег. При обработке результатов обмера сильный сбег бревен компенсируется малым. В результате оказывается, что среднеарифметические объемы, содержащиеся в таблицах объемов бревен, соответствуют их среднему сбегу. Поэтому объем бревен, имеющих средний сбег, будет определяться по таблицам наиболее точно.
Таблицы для определения объемов бревен по срединным диаметрам дают возможность в известной мере учитывать особенности сбега отдельных бревен. Из двух бревен, имеющих одинаковые диаметры в верхнем отрезе, но разный сбег, срединный диаметр окажется большим у бревна с большим сбегом. Соответственно этому фактический объему более сбежистого бревна также будет больше, чем у малосбежистого.
Схема бревен с разным сбегом.
При пользовании таблицами для определения объемов бревев по диаметрам в верхнем отрезе различие в сбеге учесть нельзя: бревна с разным сбегом, но одинаковыми диаметрами в верхнем отрезе будут одинаковыми по объему.
Наибольшие отклонения в сбеге по сравнению с бревнами, для которых составлены таблицы, будут иметь малосбежистые и сильносбежистые бревна, поэтому при определении объемов таких бревен по таблицам получатся наибольшие ошибки. Объемы сильносбежистых бревен таблицы преуменьшают, а малосбежистых — преувеличивают. С увеличением длины бревен в обоих случаях расхождение фактических объемов с табличными увеличивается.
При приемке больших партий бревен, среди которых есть малосбежистые, сильносбежистые и со средним сбегом, таблицы, по которым объемы определяют по длине и верхнему отрезку, дают удовлетворительные результаты: преуменьшение объемов одних бревен перекрывается преувеличением других и в среднем получается объем, близкий к действительному.
Для таксации бревен в прошлом применялись таблицы объемов бревен Арнольда, Тура, Турского, Рудзкого, Климашевского, Орлова и др.
Более обширный фактический материал был использован при составлении таблицы объемов бревен для разных пород под руководством лесничего А. А. Крюденера. Для сосновых и еловых бревен составлены таблицы по отдельным разрядам сбега и особые таблицы для комлевых и некомлевых бревен. В результате всестороннего изучения вопроса о таксации бревен Крюденер пришел к выводу, что для определения объемов бревен всех пород пригодна таблица объема бревен, составленная им для еловых комлевых бревен по одному среднему сбегу. В этой таблице для диаметров в верхнем отрезе через каждую четверть вершка (1,12См) И для длины через каждый аршин (0,711М) Ствола даны объемы в кубических футах.
Таблицы объемов бревен были составлены Крюденером на основе его же таблиц объемов и сбега стволов, определяющих диаметры стволов от комля к вершине через каждые 2 аршина длины стволов.
При составлении таблиц объемов бревен стволы разных размеров он условно делил на отдельные бревна и применительно к диаметрам в разных сечениях находил их объемы. Для бревен, имеющих одинаковые длину и диаметр в верхнем отрезе, но полученных из разных стволов, находили среднеарифметические объемы. Среднеарифметические объемы бревен и их диаметры в верхнем отрезе для бревен одной длины наносили на график, и получались кривые объемов для каждой ступени длины бревен. При окончательном определении объемов кривые выравнивали.
Таблицы объемов бревен Крюденера были переведены в 1926г. проф. Г. М. Турским в метрические меры и с тех пор стали называться таблицами Крюденера — Турского.
2. Составление массовых таблиц по методу Н. В. Третьякова.
Сортиментно-сортные таблицы проф. Н. В. Третьякова
В 1935г. проф. Н. В. Третьяковым предложены были для товарной таксации лесосечного фонда сортиментно-сортные таблицы. Эти таблицы составлены на основе некоторых закономерностей в строении древостоев, и, как видно из их названия, по ним можно выявлять не только сортиментацию леса на корне, но и сортность лесоматериалов.
Для использования сортиментно-сортных таблиц необходимо, во-первых, чтобы таксируемая единица (для простоты будем называть ее делянкой) была однородна в лесотаксационном отношении, т. е. состояла только из одного лесотаксационного участка. Если в пределах делянки можно усмотреть два и более таксационных участков, то их необходимо четко обособить друг от друга визирными линиями и таксировать по отдельности. Во-вторых, в делянках необходим подеревный перечет по элементам леса и с подразделением деревьев на категории деловых, полуделовых (фаутных) и дровяных.
После перечета делянки определяют разряд высоты для каждой ее породы. Для нахождения разряда отбирают в ступенях толщины (кроме крайних, как наиболее малочисленных) по три дерева, средних по высоте; их измеряют высотомером, находят среднеарифметические высоты и записывают в перечетной ведомости против соответствующих ступеней толщины. Далее, по ступеням толщины и средним их высотам вычерчивают на миллиметровой бумаге график кривой средних высот ступеней. Получившуюся вначале ломаную сглаживают обычным порядком и сравнивают с кривыми высот разных разрядов массовых объемных таблиц, по которым работают; к графику какого разряда таблиц она окажется ближе, тот разряд и будет разрядом древостоя.
дерева, средних по высоте; их измеряют высотомером, находят среднеарифметические высоты и записывают в перечетной ведомости против соответствующих ступеней толщины. Далее, по ступеням толщины и средним их высотам вычерчивают на миллиметровой бумаге график кривой средних высот ступеней. Получившуюся вначале ломаную сглаживают обычным порядком и сравнивают с кривыми высот разных разрядов массовых объемных таблиц, по которым работают; к графику какого разряда таблиц она окажется ближе, тот разряд и будет разрядом древостоя.
По разряду высоты находят соответствующую ему таблицу объемов из местных массовых таблиц и приступают к выявлению запаса в коре для каждой ступени толщины древостоя. Выявленные запасы заносят в специальную перечетно-сортиментную ведомость, отдельно для каждой категории деревьев деловых, полуделовых (фаутных) и дровяных.
Выход лесоматериалов из запаса делянки определяют по сортиментно-сортным таблицам.
В сортиментно-сортных таблицах выход сортиментов и их сортность указаны для каждой ступени, толщины по отдельности в процентах от ее запаса в коре, но выход лесоматериалов исчисляется таблицами в ликвидном виде, т. е. без коры, за исключением дров. Сортность для таблиц устанавливается согласно существующим ОСТ. К разделу прочих сортиментов в таблицах отнесены жерди, колья и тарные кряжи, а к отходам — вершинки и кора от деловых стволов.
Таким образом, для таксации делянки по сортиментно-сортным таблицам необходимо иметь:
1) подеревный сплошной перечет по каждому древостою элемента леса и его разряд высоты;
2) запасы древесины по каждой ступени толщины и для каждой
категории деревьев: деловых, полуделовых (фаутных) и дровяных по отдельности.
Располагая перечисленными таксационными признаками, можно, подобрав по разряду высоты соответствующую сортиментно-сортную таблицу, выявить по ее процентным показателям выход сортиментов в кубических метрах.
Сотиментно-сортные таблицы очень оригинальны по идее, но по сути это целевые сортиментные таблицы; по ним можно выявить наличие в лесу только тех сортиментов, которые перечислены в таблицах, и нет возможности определить выход тех, которые в них отсутствуют. Таблицы еще недостаточно проверены.
3. Закономерное распределение деревьев по толщине в однородных насаждениях.
Распределение числа деревьев по ступеням толщины дает общее представление о строении насаждения. Последнее оказывается наиболее наглядным при построении графиков. При этом по оси абсцисс обычно откладывают ступени толщины, а по оси ординат — количество деревьев в соответствующих ступенях толщины. Соединение полученного ряда точек дает кривые распределения деревьев по толщине.
При построении такого рода графиков для простых, чистых, одновозрастных насаждений получаем одновершинное распределение.
На графике, построенном для насаждения, в котором длительное время ведутся выборочные рубки (выборочный лес — Plenter-wald), наблюдается убывающее распределение.
В одновозрастных, чистых насаждениях, созданных путем посева и посадки и имевших до смыкания крон деревьев одинаковый уход (уборку отстающих в росте деревьев), распределение деревьев по толщине характеризуется симметричной, одновершинной линией, называемой кривой нормального распределения. В этом случае влияния многочисленных факторов, задерживающих и способствующих росту деревьев, взаимно уравновешиваются.

0,5 0,7 0.9 1,1 1,3 1,5 1,7
0,6 0,8 1,0 1,7 1,4 1,6
Распределение деревьев по
ступеням толщины, %
Чистые, одновозрастные насаждения после смыкания крон деревьев сохраняют до высокого возраста, а иногда и всю жизнь одновершинное распределение, в основе которого лежит кривая нормального распределения. Однако довольно часто после смыкания крон у кривых распределения появляется асимметрия. Она есть следствие конкуренции между деревьями. Более крупные деревья, занимающие в насаждении лучшее положение, имеют все преимущества для успешного роста, и поэтому характеризующая их правая ветвь кривой распределения становится длиннее. Левая ветвь, изображающая отстающие в росте деревья, становится более короткой из-за отпада ослабленных деревьев или в результате вырубки отстающих в росте деревьев в порядке ухода за насаждением. Таким образом, на графике наблюдается асимметрия. В последующем асимметрия уменьшается или остается неизменной.
В связи с изложенным одновершинная, асимметричная кривая характеризует молодое насаждение или пройденное рубками ухода по так называемому низовому способу, направленному на уборку отстающих в росте деревьев.
Многие исследователи (Назлунд, Леннрот, Продан и др.) предложили для характеристики указанного строения насаждений кривую Шарлье.
По мере увеличения возраста насаждения растет размах распределения деревьев по толщине. Из-за уменьшения числа деревьев в насаждении кривая становится более плоской.
С увеличением возраста насаждения характер распределения деревьев изменяется в зависимости от древесной породы и хода изреживания.
В результате конкуренции между деревьями они разделяются на классы роста и развития и в конечном итоге образуются главный и подчиненный полог (главная и подчиненная часть насаждения). В этом случае в кривой распределения деревьев по толщине образуется двухвершинность.
Изреживание верхнего полога и вырубка при уходе за лесом деревьев средних размеров также ведут к двухвершинности в распределении.
Распределение деревьев по толщине в смешанных насаждениях, состоящих из светолюбивой и теневыносливой древесных пород, также характеризуется вершинными кривыми.
По исследованиям Назлунда, двухвершинное распределение деревьев может быть характеризовано несколькими нормальными кривыми.
Насаждения, в которых ведутся выборочные рубки (Plenter-wald), имеют экстремальную (убывающую) форму распределения. Для таких насаждений свойствен большой размах распределения: от 0 до 70См И больше.
Между убывающим распределением и распределением, свойственным чистым, простым, одновозрастным насаждениям, наблюдаются промежуточные формы распределения.
Девственный лес, а также насаждения, состоящие из семенных и порослевых деревьев, характеризуются усложненными кривыми с несколькими вершинами.
Перечет деревьев, отображающий форму распределения деревьев по толщине, характеризует лесоводственную структуру насаждения.
Знание закономерностей распределения деревьев по толщине облегчает определение выхода сортиментов из насаждения. Решение этой задачи особенно облегчается в отношении чистых, простых, одновозрастных насаждений, а также и для типичных выборочных насаждений.
В конце прошлого века немецкий проф. В. Вейзе, изучая вопрос о среднем диаметре деревьев, пришел к выводу, что число деревьев меньше средней толщины составляет в насаждении 57,5% от их общего числа, а больше средней толщины — 42,5%. Таким образом, среднее по толщине дерево как бы делит все имеющиеся в насаждении деревья на две неравные части.
Закономерность, обнаруженная проф. В. Вейзе, была подтверждена позднейшими исследованиями, причем было установлено, что она наблюдается у всех древесных пород. Эта закономерность, определяющая место среднего дерева в насаждении, имеет теоретическое и практическое значение, так как облегчает нахождение среднего диаметра насаждения.
Допустим, что в результате обмера в насаждении оказалось следующее распределение деревьев по ступеням толщины: ступени
Толщины, См 12 16 20 24 28 32 36 40 44 48 Итого число деревьев 15 45 100 190 215 205 11О 80 30 10 1000
В соответствии с найденной закономерностью 575 деревьев должны иметь диаметр меньше среднего, а остальные 425 деревьев — больше среднего.
Чтобы найти величину среднего диаметра, будем складывать число деревьев более тонких ступеней, пока не наберем 575 шт. В ступенях толщины от 12 до 28См Их оказалось 15 + 45 + + 100 + 190 + 215 = 565 деревьев. До заданного количества (575) нам недостает 10 деревьев. Их надо взять из ступени толщины 32См. К этой ступени толщины относятся деревья от 30,1 до 34См. Всего в ней имеется 205 деревьев; у более тонких деревьев диаметр лишь на несколько десятых сантиметра будет превышать 30См, А округленно будет равен 30См. Следовательно, у последних 10 деревьев, которые тоньше среднего дерева, диаметр округленно также равен 30См.
Все остальные деревья толще среднего дерева, значит, граница между деревьями этих двух групп близка к 30См. Отсюда следует, что в данном случае средний диаметр насаждения, разграничивающий деревья на две группы, также близок к 30См.
Изучением закономерностей распределения деревьев в насаждениях по толщине занимался также венгерский проф. Фекете. На основании материалов, полученных в результате исследования еловых насаждений, он составил таблицу, в которой даны средние диаметры, кратные 5См (10; 15; 20; 25См И т. д.), затем диаметр самого тонкого дерева в насаждении, далее — диаметр дерева, отграничивающего первые 10% более тонких деревьев в насаждении, 20; 30% и т. д. через каждые 10%.
Составив такую таблицу, проф. Фекете пришел к следующему выводу. Если в насаждении заданного среднего диаметра отсчитать определенное число деревьев, выраженное в процентах от их общего числа (причем счет деревьев вести начиная с самого тонкого), то у дерева, отграничивающего отсчитанный процент деревьев, диаметр будет определенной величиной.
Допустим, что насаждение имеет средний диаметр 25См. Согласно таблице проф. Фекете диаметр самого тонкого дерева в насаждении равен 13,8См. Если в этом насаждении отобрать 10% самых тонких деревьев, то толщина последнего дерева, которое войдет в первые 10%, будет равна 17,3См; Если отобрать 20% более тонких деревьев, то дерево, отграничивающее эти 20%, будет иметь диаметр 19,3См; Если отсчитать 30% более тонких деревьев, то диаметр самого толстого дерева, входящего в эти 30%, будет равен 20,8См И т. д.
Такие вычисления были произведены проф. Фекете для насаждения разных средних диаметров; им указаны в абсолютных числах (сантиметрах) диаметры деревьев, отграниченных от самого тонкого дерева на величину, кратную 10%.
Более широко обобщил распределение деревьев в насаждениях по диаметру австрийский лесовод Шиффель, который выразил диаметры не в абсолютных числах, а в долях средних диаметров насаждений (Rd).
Такие относительные значения диаметров в лесной таксации названы редукционными числами по диаметру. Иными словами, редукционное число по диаметру Rd есть частное от деления диаметра того или иного дерева на диаметр среднего дерева.
Замена абсолютных значений диаметров относительными величинами позволяет в насаждениях разных средних диаметров сравнивать толщину деревьев, растущих в одинаковых условиях.
Все деревья, составляющие насаждение, Шиффель распределил в последовательный ряд — по возрастанию диаметров.
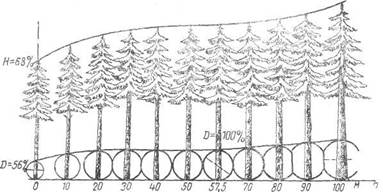
H=114%
место дерева в насаждении
Среднее дерево
Схема распределения деревьев по размерам и их месту в насаждении
Этот ряд он разделил на десять частей. Для деревьев, оказавшихся на границе каждого из десяти отрезков, были найдены диаметры, выраженные в долях среднего диаметра, и в итоге составлена таблица редукционных чисел.
Редукционные числа по диаметру (Rd) для еловых насаждений
(по данным Шиффеля)
|
Средний диаметр,
см
|
Диаметры в долях среднего диаметра, отграниченные от низшей ступени на число
Процентов от общего числа деревьев
|
|
|
|
|
|
|
|
0
|
10
|
20
|
30
|
40
|
50
|
60
|
70
80
|
80
|
90
|
100
|
|
|
10
0,540
|
0,540
|
0,710
|
0,770
|
0,810
|
0,850
|
0,910
|
0,970
|
1,07
|
1,15
|
1,28
|
1,95
|
|
|
15
0,547
|
0,547
|
0,700
|
0,766
|
0,827
|
0,871
|
0,933
|
0,983
|
1,07
|
1,17
|
1,28
|
1,77
|
|
|
20
|
0,550
|
0,695
|
0,770
|
0,830
|
0,885
|
0,940
|
1,005
|
1,07
|
1,17
|
1,29
|
1,67
|
|
|
25
|
0,552
|
0,692
|
0,772
|
0,832
|
0,892
|
0,948
|
1,010
|
1,08
|
1,17
|
1,28
|
1,61
|
|
|
30
|
0,553
|
0,690
|
0,771
|
0,838
|
0,893
|
0,953
|
1,010
|
1,08
|
1,17
|
1,28
|
1,57
|
|
|
35
|
0,555
|
0,689
|
0,771
|
0,838
|
0,897
|
0,958
|
1,010
|
1,08
|
1,17
|
1,28
|
1,55
|
|
|
40
|
0,555
|
0,687
|
0,772
|
0,840
|
0,900
|
0,960
|
1,020
|
1,08
|
1,17
|
1,28
|
1,52
|
|
|
45
|
0,557
|
0,687
|
0,771
|
0,842
|
0,902
|
0,962
|
1,020
|
1,08
|
1,17
|
1,28
|
1,51
|
|
|
50
|
0,556
|
0,686
|
0,774
|
0,842
|
0,900
|
0,964
|
1,020
|
1,09
|
1,17
|
1,28
|
1,49
|
|
|
Средние вычисленные по формуле
|
0,555
|
0,689
|
0,771
|
0,837
|
0,895
|
0,955
|
1,010
|
1,08
|
1,17
|
1,281
|
1,55
|
|
|
0,555
|
0,680
|
0,771
|
0,841
|
0,898
|
0,948
|
1,006
|
1,078
1,173
|
1,173
|
1,302
|
1,475
|
|
Из таблицы видно, что диаметры деревьев, находящихся в древостое в одинаковых условиях, составляют определенную долю от среднего диаметра, иными словами, имеют одинаковые редукционные числа. Отклонения от этого правила наблюдаются лишь у насаждений со средним диаметром менее 20См. Поэтому при выведении средних величин первые два ряда цифр не были приняты во внимание.
Наличие у насаждений общности в распределении деревьев по толщине, высоте и форме стволов принято называть закономерностями в строении насаждений.
Закономерности в строении насаждений, подтверждаемые таблицей выведены для еловых насаждений, однако они характерны и для других пород. Проф. М. В. Давидов в 1951г. получил средний ряд редукционных чисел по диаметру для буковых насаждений Закарпатской обл., характер изменения которых в общем аналогичен найденному Шиффелем. Расхождение в цифрах для крайних размеров бука — следствие некоторой разновозрастности буковых древостоев.
Редукционные числа для буковых насаждений Закарпатской обл.
(по данным М. В. Давидова)
|
Процентные доли от общего числа стволов
|
Редукционные числа
Rd
|
Процентные доли от общего числа стволов
|
Редукционные числа
Rd
|
|
0
|
0,474
|
60
|
1,00
|
|
10
|
0,611
|
70
|
1,08
|
|
20
|
0,715
|
80
|
1,18
|
|
30
|
0,787
|
90
|
1,39
|
|
40
|
0,863
|
100
|
1,85
|
|
50
|
0,935
|
-
|
-
|
Зная средний диаметр насаждения, при помощи редукционных чисел можно без труда найти диаметр дерева, занимающего то или иное положение в насаждении.
Допустим, нужно протаксировать буковое насаждение, имеющее средний диаметр 30См. Нас интересует диаметр дерева в ряду, отстоящего от самого тонкого дерева в насаждении на 40%.
По данным проф. Давидова, редукционное число у такого дерева равно 0,863. Умножив его на средний диаметр насаждения, находим, что это дерево имеет диаметр
D40 = RdD = 0,863 х 30 = 25,9См.
Исследования Вейзе, Фекете и Шиффеля дали лишь некоторые теоретические обобщения по вопросу о строении насаждений. Советские ученые пришли к новым теоретическим обобщениям и разработали на основе закономерностей строения насаждений более совершенные методы учета древесных запасов и выхода сортиментов, широко используемые в современной таксационной практике.
Проф. А. В, Тюрин для выявления закономерностей в строении насаждений распределял деревья по ступеням толщины, выраженным в десятых долях среднего диаметра насаждения (Rd). Такие ступени, являющиеся общими для всех насаждений и не зависящие от конкретных диаметров, он назвал естественными ступенями толщины. Распределение деревьев в насаждении по естественным ступеням толщины приведено в таблице.
Распределение деревьев в насаждении по естественным ступеням толщины (по данным А. В. Тюрина)
|
Естественные ступени
Толщины в долях от
Среднего диаметра
|
Число деревьев в ступени, % От их общего
Числа в насаждении
|
Естественные ступени
Толщины в долях от среднего диаметра
|
Число деревьев в ступени, % От их общего
Числа в насаждении
|
|
0,5
|
0,7
|
1,2
|
8,9
|
|
0,6
|
3,5
|
1,3
|
6,3
|
|
0,7
|
9,5
|
1,4
|
3,3
|
|
0,8
|
16,1
|
1,5
|
1,5
|
|
0,9
|
18,4
|
1,6
|
0,5
|
|
1,0
|
18,1
|
1,7
|
0,1
|
|
1,1
|
13,1
|
—
|
—
|
Среднее распределение деревьев в процентах по естественным ступеням толщины было получено проф. А. В. Тюриным в результате анализа многочисленных перечетов деревьев. Замена ступеней, выраженных в сантиметрах, относительными значениями дала возможность сравнивать и выявлять общий характер перечетов деревьев в насаждениях различных средних диаметров. Проф. А. В. Тюрин пришел к выводу, что распределение деревьев по естественным ступеням толщины не зависит ни от породы, ни от бонитета, ни от полноты насаждений. Это распределение лишь в некоторой степени зависит от возраста насаждений и в большой мере — от характера рубок ухода.
Полученное проф. Тюриным распределение деревьев по естественным ступеням толщины является обобщенным вариационным рядом, характеризующим изменчивость толщины деревьев в насаждениях и степень заселенности отдельных ступеней, составляющих определенную долю от среднего диаметра. Средние диаметры деревьев в различных насаждениях могут быть разными. Однако в строении их наблюдаются общие черты, выражающиеся в том, что в ступенях толщины, составляющих одинаковые доли от среднего диаметра, число деревьев (в процентах) оказывается близким.
М. Продан подробно рассматривает характер распределения деревьев в насаждении по их размерам. Этому распределению, по его мнению, свойственна асимметрия. После смыкания насаждения правая асимметрия, характерная для более молодых насаждений, сменяется левой, которая или остается постоянной, или сглаживается с возрастом. По заключению М. Продана, в результате дифференциации деревьев на классы роста
Возникает третий тип разделения - двухвершинное. Распределение деревьев в смешанных насаждениях также носит ярко выраженный двухвершинный характер. Выборочному лесу свойственна убывающая кривая распределения. В очень старом лесу наблюдается двухвершинное распределение.
Ян Галай, опубликовавший свою работу в 1957г., исследование провел в отношении 6 древесных пород: ели, сосны, пихты, дуба, бука и граба. При выравнивании кривых распределения им была использована функция А. Шарлье. Ян Галай справедливо отмечает, что характер распределения деревьев зависит от способа ухода за насаждением. В связи с этим для низового и верхового способов ухода за лесом он дает отдельные ряды распределения. В приведенном нами сопоставлении взят средний ряд, выведенный Яном Галаем.
Естественные ступени толщины – 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7
Число деревьев, %:
По А. В. Тюрину - 7 35 95 161 184 181 131 89 63 33 15 5 1
По Я. Галаю 3 17 49 100 152 180 168 129 86 53 32 18 9 4
Сопоставление двух рядов распределения деревьев по толщине, полученных в итоге исследований, позволяет заключить, что эти два ряда близки друг к другу. Имеющиеся некоторые расхождения в отдельных ступенях толщины существенного практического значения не имеют.
Если подсчитать по данным проф. А. В. Тюрина и Я. Галая число деревьев в %, начиная от самой тонкой ступени и до середины ступени, характеризующей средний диаметр, то получим следующий результат сложения:
Естественные ступени толщины…… 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Число деревьев, % :
По А. В. Тюрину........ - 7 35 95 161 184 181:2 = 57,25
По Я. Галаю............... 3 17 49 100 152 180 168:2 = 58,5
Приведенный расчет показывает, что, по данным А. В. Тюрина, в насаждении имеется 57,25% деревьев тоньше среднего дерева и 42,75%—толще среднего дерева. По данным Я. Галая, на первую из этих групп деревьев приходится 58,5%, а на вторую — 41,5%. Цифры обоих исследователей близки между собой.
Проф. А. В. Тюрин подсчитал суммы площадей сечений деревьев тоньше и толще среднего дерева. Оказалось, что у деревьев тоньше среднего дерева сумма площадей сечений составляет 40,35%, или округленно 40%, от площади сечения всех деревьев в насаждении, а у деревьев толще среднего дерева —59,65%, или округленно 60%.
Аналогичной дополнительной обработке нами были подвергнуты данные Я. Галая. При этом площадь сечения деревьев, имеющих толщину, меньшую среднего диаметра, оказалась равной 40,4%, а превышающих средний диаметр — 59,6%. Таким образом, данные обоих исследователей практически совпали между собой.
Распределение деревьев по естественным ступеням толщины имеет определенное преимущество. Оно является общим для всех насаждений, от него можно перейти к ступеням, измеряемым в любых мерах. Для этого надо построить график: по оси абсцисс отложить естественные ступени толщины, а по оси ординат — последовательные суммы числа деревьев, соответствующие естественным ступеням толщины, нанесенным по оси абсцисс.
По исследованиям проф. Тюрина, наименьшей естественной: ступенью толщины оказалась ступень 0,5. Против верхней границы этой ступени, т. е. против 0,55, откладываем на графике процент деревьев, равный в этой ступени 0,7. Верхней границей следующей ступени, равной 0,6, будет 0,65. Против абсциссы, соответствующей 0,65, наносим процент деревьев, оказавшийся в этой ступени, плюс процент деревьев естественной ступени 0,5. Против верхней границы естественной ступени 0,7 откладываем суммарный процент деревьев по трем ступеням толщины: 0,5; 0,6; 0,7.
Установив в отмеченной последовательности длину ординат и соединив нанесенный на график ряд точек, получим кривую последовательного суммирования деревьев по ступеням толщины в %. Такая кривая в статистике называется огивой.
Чтобы на основании этого графика найти распределение деревьев по конкретным ступеням толщины при определенном среднем диаметре насаждения, отрезок абсциссы, заключенный между крайними ординатами, нужно разделить на столько мелких отрезков, сколько сантиметров содержится в диапазоне от самого тонкого до самого толстого дерева.
Допустим, что нужно установить распределение деревьев по ступеням толщины в насаждении со средним диаметром 20См. Согласно приведенным выше расчетам самые тонкие деревья низшей ступени толщины имеют диаметр, равный 0,45 величины среднего диаметра, а предельный диаметр деревьев самой высшей ступени в 1,75 раза выше среднего. В нашем примере, следовательно, самые тонкие деревья будут иметь диаметр 20см х 0,45 = 9См, А самые толстые 20См Х 1,75 = 35См.
Между этими двумя крайними размерами толщины содержится 35 — 9 = 26 односантиметровых ступеней. Соответственно этому отрезок абсциссы, ограничиваемый кривой, следует разделить на 26 частей. Против точки пересечения кривой осью абсцисс ставим цифру 9, а против ординаты противоположного конца кривой — цифру 35. В этих пределах разместим все прочие односантиметровые ступени толщины. Деления на оси абсцисс, соответствующие 10; 14; 18; 22; 26См И т. д., являются границами четырехсантиметровых ступеней толщины.
Длина ординаты, соответствующая на абсциссе делению 10См, Будет определять процент деревьев в ступени 8См. Для получения процента деревьев в ступени 12См Надо из длины ординаты У14, Соответствующей делению на абсциссе, равному 14См, Вычесть длину ординаты У14, Идущую от деления 10 См:
Р12 = У14 — У10
Процент деревьев в ступени толщины 16См Равняется разности в длине ординат, идущих от делений 18 и 14См:
Р10 = У18 — У14
Таким же образом определяется заселенность всех прочих четырехсантиметровых ступеней толщины.
На основании этого примера можно сделать вывод, что процент деревьев в первой ступени толщины определяется длиной ординаты, взятой против верхней границы первой ступени толщины. Для определения процента деревьев во всех последующих ступенях толщины надо взять длину ординат, соответствующих верхним границам ступеней, и из длины ординаты верхней границы ступени вычесть длину ординаты нижней границы ступени:
Рп = Уп — Уп-1
Во всех случаях длина ординат измеряется с учетом масштаба графика.
Подобные расчеты производят для насаждений различных средних диаметров. В зависимости от величины среднего диаметра насаждения и разницы между более толстым и тонким деревом насаждения отрезок абсциссы делят на определенное число частей. Результаты расчетов сводят в таблицу распределения деревьев по четырехсантиметровым ступеням толщины в зависимости от среднего диаметра насаждений.
Распределение деревьев преобладающей части насаждения по четырехсантиметровым ступеням толщины
(по данным проф. А. В. Тюрина)
|
Средний диаметр насаждения, см
|
Ступени толщины, См
|
|
8
| 12
|
12
|
16
|
20
|
24
|
28
|
32
|
36
|
40
|
44
|
48
|
52
|
56
|
60
|
|
Число деревьев, %
|
|
|
20
|
0,5
|
8,7
|
30,1
|
33,9
|
18,5
|
7,1
|
1,2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
22
|
-
|
4,9
|
19,0
|
31,9
|
26,7
|
12,7
|
4,5
|
0,3
|
-
|
-
|
-
|
-
|
-
|
-
|
|
24
|
-
|
2,0
|
12,2
|
27,5
|
29,3
|
17,6
|
8,7
|
2,4
|
0,3
|
-
|
-
|
-
|
-
|
-
|
|
26
|
-
|
0,7
|
7,8
|
21,7
|
27,7
|
21,5
|
12,5
|
5,7
|
2,4
|
-
|
-
|
-
|
-
|
-
|
|
28
|
-
|
0,4
|
4,6
|
15,3
|
24.4
|
24,3
|
16,0
|
9,5
|
4,2
|
1,2
|
0,1
|
-
|
-
|
-
|
|
30
|
-
|
-
|
2,7
|
10,5
|
19,7
|
24,7
|
19,2
|
12,6
|
6,6
|
3,2
|
0,8
|
-
|
-
|
-
|
|
32
|
-
|
-
|
3,3
|
8,8
|
15,4
|
22,6
|
21,4
|
13,6
|
9,3
|
5.2
|
1,8
|
0,5
|
0,1
|
-
|
|
34
|
-
-| —
|
-
|
0,6
|
4,7
|
11,8
|
19,7
|
21,2
|
17,5
|
11,4
|
7,2
|
3,8
|
1,6
|
0,5
|
-
|
|
36
|
-
|
-
|
0,2
|
3,1
|
8,7
|
16,2
|
19,6
|
19,1
|
13,8
|
9,2
|
5,7
|
2,8
|
1,1
|
0,5
|
Построив второй график, на котором по оси ординат в возрастающем порядке будут отложены суммы площадей поперечных сечений, можно составить таблицу распределения сумм площадей поперечных сечений деревьев в насаждениях по четырехсантиметровым ступеням толщины.
Распределение сумм площадей поперечных сечений деревьев
Преобладающей части насаждения по четырехсантиметровым ступенямтолщины (по данным проф. А. В. Тюрина)
|
Средний диаметр насаждения, см
|
Ступени толщены, см
|
|
8
|
12
|
16
|
20
|
24
|
28
|
32
|
36
|
40
|
44
|
48
|
52
|
56
|
60
|
|
Суммы площадей сечений, %
|
|
20
|
0,1
|
3,1
,1
|
19,3
|
33,9
9
|
26,6
|
13,9
9
|
3,1
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
22
|
-
|
1,4
,4
|
10,0
|
26,3
3
|
31,5
|
20,5
|
9,5
|
0,8
|
-
|
-
|
-
|
-
|
-
|
-
|
|
24
|
-
|
0,5
,5
|
5,4
|
19,0
0
|
29,4
|
24,0
0
|
15,5
|
5,4
|
0,8
|
-
|
-
|
-
|
-
|
-
|
|
26
|
-
|
0,2
,2
|
2,9
|
12,8
8
|
23,6
|
24,8
8
|
19,0
|
11,0
|
5,7
|
-_
|
-
|
-
|
-
|
-
|
|
28
|
-
|
0,1
1
|
1 5
|
7,8
|
17,9
|
24,4
4
|
20,8
|
15,7
|
8,6
|
2,9
9
|
0,3
3
|
-
|
-
|
-
|
|
30
|
-
|
-
|
0,8
|
4,7
7
|
12,6
|
21,4
4
|
21,8
|
18,1
|
11,7
|
6,9
,9
|
2,0
0
|
-
|
-
|
-
|
|
32
|
-
|
-
|
0,3
|
2,7
7
|
8,6
|
17,3
3
|
21,4
|
19,8
|
14,5
|
9,8
8
|
4,0
0
|
1,3
|
0,3
О
|
-
|
|
34
|
-
|
-
|
0,1
|
1,6
6
|
5,9
|
13,4
4
|
18,8
|
19,6
|
15,8
|
12,1
|
7,6
6
|
3,7
|
1,4
4
|
-
|
|
36
|
-
|
|
-
|
0,9
9
|
3,9
|
9,8
8
|
15,4
|
19,1
|
17,0
|
13,8
,8
|
10,2
2
|
5,8
|
2,7
7
|
1,4
|
В однородных насаждениях суммы площадей поперечных сечений по отдельным ступеням толщины почти прямо пропорциональны запасам древесины в этих ступенях. Поэтому таблицу можно использовать для распределения по ступеням толщины не только сумм площадей поперечных сечений, но и запасов насаждений.
Таблицы, дающие распределение по ступеням толщины общего числа деревьев, образующих насаждение, и сумм площадей их поперечных сечений, имеют в таксации большое практическое значение.
На основании этих таблиц и данных глазомерной таксации можно ориентировочно, не производя перечета, распределить число деревьев и запас насаждения по ступеням толщины.
Чтобы воспользоваться таблицей, сначала нужно определить число деревьев при помощи таблиц хода роста насаждений. Найденное число деревьев распределяют по ступеням толщины, как и запас насаждения.
Эти таблицы служат также основой для составления так называемых товарных таблиц, в которых приведено распределение запаса насаждений по сортиментам.
Закономерное распределение деревьев по толщине является основой учета древесных запасов и широко используется для расчленения насаждений на составные части, а также для их промышленной оценки.
В однородных насаждениях деревья по своей толщине делятся на такое число четырехсантиметровых ступеней толщины, которое равняется 3/8 величины среднего диаметра насаждения. Допустим, что средний диаметр насаждения равен 24См. От этой величины 3/8 составляют 24х3/8 = 9. Следовательно, в этом насаждении имеются деревья, относящиеся к 9 четырехсантиметровым ступеням толщины.
В однородных насаждениях, не затронутых рубками, изменчивость толщины деревьев характеризуется коэффициентом вариации, в среднем равным 30%.
По данным М. Л. Дворецкого, в насаждениях разных возрастов изменчивость диаметров характеризуется следующими коэффициентами вариации:
Возраст насаждений, лет…………………...26 45 60 64 80 155
Коэффициенты вариации диаметров, %...... 41 38 30 34 24 23
Из этих цифр видно, что с увеличением возраста насаждений коэффициенты вариации диаметров уменьшаются.
Внутри четырехсантиметровых ступеней толщины распределение деревьев по более мелким градациям в толщине неравномерное, что подтверждается данными проф. Н. В. Третьякова. В ступенях толщины, меньших, чем величина среднего диаметра насаждения, преобладают деревья, находящиеся во второй половине ступени. В ступенях толщины, превышающих по своей величине средний диаметр насаждения, большая часть деревьев находится в первой половине ступени, т. е. имеет более мелкие диаметры.
Для всех ступеней толщины, взятых в целом, процент деревьев, приходящихся на первую и вторую половину ступеней, почти одинаков.
В ФРГ рассматриваемый вопрос изучал М. Продан. Он обнаружил три типа распределения деревьев в ступени: равномерное, возрастающее и убывающее. Во всех этих трех типах отклонение среднего диаметра деревьев от середины ступени не превышает 5%.
К таким же выводам пришел X. Майер, изучавший этот вопрос в выборочном лесу.
4. Средний и текущий прирост.
Увеличение с течением времени древесной массы в дереве или в насаждении — следствие изменения величины диаметров деревьев, их площадей сечения, высот и видовых чисел. Поэтому при рассмотрении вопроса об изменении древесной массы следует изучить методы определения прироста по всем перечисленным таксационным показателям,
В лесной таксации различают два вида прироста: средний и текущий.
Средним приростом считают величину, на которую в среднем в единицу времени (чаще всего год) на протяжении всей жизни дерева или насаждения изменяется абсолютная величина одного из перечисленных выше таксационных показателей. Средний прирост определяется путем деления абсолютной величины таксационного показателя на возраст дерева.
Текущий прирост представляет собой величину, на которую изменяется данный таксационный показатель в определенное время жизни дерева, например за последний год. Он определяется как разность в величине того или иного таксационного показателя в данный момент и год назад.
Величину изменения таксационных показателей дерева за год точно измерить трудно, так как она весьма незначительна, а таксационные измерения имеют невысокую точность. Поэтому чаще всего текущий годичный прирост определяют по разности таксационных показателей не за один год, а за П Лет (5; 10 и т. д.). Например, текущий годичный прирост по объему принимают равным разности в объемах дерева, наблюдаемых в данное время и 10 лет назад, разделенной на 10.
При таком определении получают вместо текущего средний годичный прирост, наблюдаемый в последний период жизни дерева. Таким образом, теоретическое представление о текущем приросте несколько отличается от фактически устанавливаемого прироста.
Так как при таксации леса вместо прироста за последний год определяется прирост за определенный период П Лет, его называют периодическим.
Однако величина периодического прироста мало показательна для суждения об успешности роста отдельного дерева или целого насаждения. Поэтому величину периодического прироста делят на число лет П В этом периоде.
Текущий прирост дерева обозначается буквой Z, Средний — Д. При определении прироста какого-нибудь таксационного признака добавляют буквы, принятые для его обозначения (по высоте H, По диаметру D, По площади сечения G, По объему V, По видовому числу F, По запасу М).
Средний и текущий приросты по всем этим таксационным показателям определяют по следующим формулам:
ДH = Hа : а; (340) ДD = Dа : а; (341)
ДG = Gа : а; (342) Дv = Vа : а; (343)
ДF = Fа : а; (344) Дм = МА : а; (345)
Zh = (Hа – Hа-п) : п; (346) Zd = (DA – DA-N) : п;(347)
Zg = (gA – gA – n) : n; (348) Zv = (VA – VA-n) : n; (349)
Zf = (fA – FA-n) : n; (350) ZM = (MA – MA-n) : n; (351)
В этих формулах
А — Возраст дерева в данное время;
A — П — возраст дерева П Лет назад.
У деревьев хвойных пород в первые 50—60 лет текущий прирост обычно больше среднего, в 50—60-летнем возрасте оба вида прироста одинаковы, а в последующий период они неизменно уменьшаются, причем более быстро падает текущий прирост. Такое соотношение между приростами, по опытным данным, закономерно, что подтверждается также приводимым ниже теоретическим расчетом.
Возьмем в жизни дерева или насаждения два момента, отделенных один от другого промежутком в 1 год. Первый момент обозначим через П, Второй через П+1. Соответственно этому текущий прирост в эти два момента обозначим через ZП и Zn+1, А средний — ДN и Дп+1.
Составим следующее уравнение для определения текущего прироста:
ZП+1 = ДN+1(N+1) - ДNN. (352)
После несложных алгебраических преобразований оно примет следующий вид:
ZN+1 - Дп+1 = (Дп+1 - ДП)п. (353)
Анализируя это уравнение, приходим к заключению, что при увеличении среднего прироста текущий прирост будет больше среднего:
Дп+1 > Д П ; Zп+1 > Дп+1,
При уменьшении — меньше среднего:
Дп+1 < ДП; ZN+1 < ДП+1,
А при неизменности среднего прироста — равен среднему:
Дп+1 = ДП; Zп+1 = ДП+1.
Отсюда можно заключить, что в изменении приростов наблюдаются два периода. В первый период средний прирост хотя и возрастает, но текущий прирост неизменно оказывается выше среднего; во второй период оба вида прироста уменьшаются, причем текущий прирост оказывается меньше среднего. В момент равенства приростов средний прирост достигает максимума, а затем начинает уменьшаться.
Максимум текущего прироста по массе наступает раньше, чем максимум среднего прироста. По абсолютной величине максимум текущего прироста больше максимума среднего, поскольку последний наступает в тот момент, когда текущий прирост перешел в стадию падения. Представление о соотношении приростов дает рисунок. Приведенное на рисунке соотношение двух кривых типично для отдельных деревьев и целых древостоев.
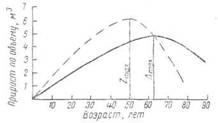
Соотношение текущего (пунктир) и среднего
(сплошная линия) приростов
В данном случае первый период в изменении приростов продолжался 63 года. В этом возрасте наступил максимум среднего прироста, который в этот момент был равен текущему приросту. Максимум текущего прироста оказался в возрасте 50 лет, т. е. на 13 лет раньше наступления максимума среднего прироста. По абсолютной величине максимум текущего прироста оказался на 20% больше максимума среднего прироста.
У отдельных деревьев и насаждений соотношения между текущим и средним приростом не всегда совпадают с рассмотренными на графике: кривые хода прироста в некоторых случаях не пересекаются вовсе или пересекаются неоднократно. Основной причиной отклонений в соотношении приростов является своеобразие жизненного процесса данного дерева или насаждения, обусловливаемое изменениями внешней среды. Например, в отдельные периоды роста дерева или насаждения могут наблюдаться резкие различия в количестве атмосферных осадков, уровне грунтовых вод в результате осушения или заболачивания данной территории, в числе окружающих деревьев, что вызывает осветление или затенение данного дерева.
Несмотря, однако, на неизбежные отклонения в соотношении приростов от рассмотренной схемы, она может служить в известной мере нормативом, который поможет вскрыть особенности развития и роста отдельных деревьев и насаждений.
5. Лесные таксы.
Загальні положення
1. Такси застосовуються під час відпуску будь-яким заготівельникам деревини лісових порід на пні в порядку рубок головного користування, суцільних санітарних та лісовідновних рубок, рубок, не пов’язаних з веденням лісового господарства (розчищення земельних ділянок, вкритих лісовою рослинністю, у зв’язку з будівництвом гідровузлів, трубопроводів, доріг тощо), а також під час заготівлі живиці.
У разі здійснення рубок догляду за лісом, вибіркових санітарних рубок, рубок пов’язаних з реконструкцією малоцінних молодників і похідних деревостанів, прокладанням просік, створенням протипожежних розривів тощо, такси застосовуються під час відпуску деревини лісових порід на пні заготівельникам, які не є постійними користувачами ділянок лісового фонду.
2. Такси на деревину лісових порід, що відпускається на пні,
застосовуються з урахуванням розподілу лісів за лісотаксовими поясами і розрядами, а саме:
А) розподіл лісів за лісотаксовими поясами:
До першого поясу віднесено всі ліси, за винятком лісів Закарпатської, Івано-Франківської, Чернівецької областей та лісів гірської зони Львівської області:
До другого поясу віднесено ліси Закарпатської, Івано-Франківської, Чернівецької областей та ліси гірської зони Львівської області;
Лісотаксові розряди встановлюються для кожного кварталу (урочища) виходячи з наведеної нижче відстані між центром кварталу і найближчим нижнім складом лісозаготівельника до якого деревина вивозиться безпосередньо з лісосіки або пунктом відвантаження деревини залізницею.
|
Лісотаксові
Розряди
|
1
|
2
|
3
|
4
|
5
|
|
Відстань, км
|
До 10
|
10,1-25
|
25,1-40
|
40,1-60
|
60,1 і більше
|
Відстань (пряма) від центру кварталу (урочища) до нижнього складу
або пункту відвантаження деревини залізницею визначається за картографічними матеріалами і може користуватися залежністю від геоморфологічних умов місцевості за такими коефіцієнтами:
У лісах з рівнинним рельєфом - 1,10
У лісах з_ горбистим рельєфом або у лісах, понад 30 відсотків площі яких зайнято болотами - 1,25
У лісах з гірським рельєфом - 1,50
Пунктом, з якого можливе відвантаження деревини залізницею, вважається пункт (залізнична станція, роз'їзд), де дозволено здійснення цієї операції, незалежно від наявності на ньому відповідних складів.
3. Зміна розподілу лісів за лісотаксовими розрядами можлива у разі:
Закриття діючих або відкриття нових пунктів (залізничних станцій чи роз'їздів) для відвантаження деревини;
Виявлення порушень встановленого порядку розподілу лісів за лісотаксовими розрядами.
4. До великої деревини всіх Лісових Порід належать відрізки стовбура У Верхньому перетині без кори діаметром від 25см і більше, до середньої — Діаметром від 13 до 24см до дрібної — діаметром від 3 до 12см.
До дровяної деревини належать сортименти, які можна використовувати для технологічних потреб, а також непридатні для промислової переробки (дрова паливні).
На дров'яну деревину, використану для технологічних потреб, донараховується плата за результатами фактичної заготівлі з урахуванням того, що загальна сума такої плати повинна становити 70 відсотків такси на ділову дрібну деревину відповідної лісової породи.
За ліквід з крони встановлюється плата в розмірі 40 відсотків, а за порубкові залишки, що підлягають використанню, - 20 відсотків такси дровяної деревини відповідної лісової породи.
Такси на Ділову і дроВ'яну деревину липи встановлені без врахування кори, а на дров'яну деревину решти лісових порід — з корою.
5. На деревину вибіркових рубок головного користування такси знижуються на 20 відсотків, а рубок, пов'язаних з веденням лісового ГоспоДарства, та інших рубок - на 30 відсотків.
Знижки у відсотках обчислюються з кожної такси окремо.
6. Рада міністрів Автономної Республіки Крим, області, Київська І Севастопольська міські державні адміністрації за поданням державних органів лісового господарства можуть у межах сум, що надходять до бюджету Автономної Республіки Крим та місцевих бюджетів, знижувати такси на деревину залежно від втрат нею технічних якостей (сухостійна, пошкоджена пожежею, комахами, грибковими хворобами, а також внаслідок бурелому, вітровалу).
7. Якщо під час відпуску деревини на пні порубкові залишки мають збут, плата за них вилучається з такс на дров'яну деревину відповідної лісової породи.
Литература
1. Н. П. Анучин Лесная таксация издательство «Лесная промышленность» Москва 1971
2. П. Н. Сергеев Лесная таксация государственное лесотехническое издательство Москва 1947 Ленинград
3. Такси на деревину лісових порід, що відпускаються на пни, і на живицю