Сетевые транспортные задачи Стз (примеры)
Сетевые транспортные задачи Стз (примеры)
|
Направление
Пути
|
Стоимость
Перевозки (Д. е.)
|
|
A1®A2
A1®A5
A2®A3
A2®A6
A3®A4
A5®A2
A5®A3
A6®A3
A6®A4
|
5
4
2
1
2
2
3
3
3
|
Сетевые транспортные задачи
Пример 3.1. Имеются два пункта A1 и A2 производства некоторого товара, причем в пункте A1 этого товара сосредоточено 10 Ед., в пункте A2 — 5 Ед. В пунктах A3 и A4 этот товар потребляется. Потребности пунктов A3 и A4 составляют соответственно 8 и 7 Ед. Доставить этот товар от производителей к потребителям можно различными путями. Имеются еще два промежуточных пункта A5 и A6, в которых возможна смена транспорта. Стоимости перевозок единицы товара из одного пункта в другой указаны в табл. 3.1.
Задача состоит в доставке товара от производителей к потребителям с минимальными суммарными транспортными расходами.
Составим математическую модель сформулированной задачи. Обозначим через Xij количество товара, перевозимого по пути Ai®Aj. Тогда, исходя из данных табл. 3.1, стоимость перевозки товара из пункта A1 в пункт A2 равна 5X12, из A1 в A5 — 4X15 и т. д. Суммарная стоимость транспортных расходов будет равна
J(X)=5X12+4X15++2X23+X26+2X34+2X52+3X53+3X63+3X64. (3.1)
Здесь X=(X12, X15, X23, X26, X34, X52, X53, X63, X64). Отразим в модели ограничения на переменные Xij. Поскольку от производителя A1 весь товар должен быть вывезен, то имеем
X12+X15=10. (3.2)
Теперь в пунктах A2 и A5 будет сосредоточено товара соответственно 5+X12 и X15. Но пункт A5 является промежуточным, в котором товар не требуется, поэтому он должен быть вывезен, т. е. согласно данным табл. 3.1 получим
X52+X53=X15. (3.3)
С учетом (3.2), (3.3) в пункте A2 объем товара увеличится и станет равным 5+X12+X52. Весь этот товар должен быть вывезен. Таким образом, с учетом путей, указанных в табл. 3.1, будем иметь
X23+X26=5+X12+X52. (3.4)
Пункт A6 тоже промежуточный, поэтому весь товар, который в него поступит, должен быть вывезен:
X63+X64=X26. (3.5)
Пункт A3 является потребителем товара, причем потребности составляют 8 Ед. Поэтому из прибывающего в этот пункт товара из пунктов A2, A5, A6 соответственно X23, X53, X63 ед. в пункте A3 остается 8 Ед., а остальной товар X34 отправляется в пункт A4. Таким образом, получим
8+X34=X23+X53+X63. (3.6)
Наконец, пункт A4 является потребителем товара. Товар в него поступает из пунктов A3 и A6, поэтому будем иметь
7=X34+X64. (3.7)
Как следует из равенств (3.2)—(3.7), для каждого из пунктов Ai суммарное количество привезенного в этот пункт товара и произведенного в нем равно суммарному количеству вывезенного из этого пункта товара и потребленного в нем. Эти условия называют Условиями баланса для каждого из пунктов. Ниже эти условия будут переписаны в удобной для дальнейших рассуждений форме.
Отметим также, что выполняются очевидные неравенства
Xij³0 (3.8)
(Xij >0, если товар перевозится по пути Ai®Aj, и Xij=0 — в противном случае).
Поскольку суммарные транспортные издержки должны быть минимальными, то функция (3.1) минимизируется по всем Xij, удовлетворяющим ограничениям (3.2)—(3.8), т. е. математическая модель задачи принимает вид (условия баланса записаны последовательно для каждого пункта Ai, 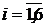 )
)
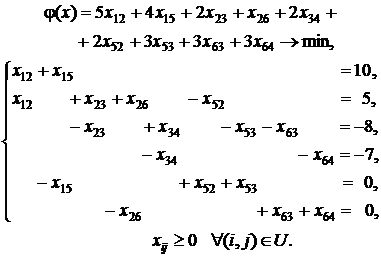 (3.9)
(3.9)
Здесь через (I, J) обозначен путь из Ai в Aj, U — множество всех путей, по которым можно перевезти товар.
Как видим, задача (3.9) является задачей ЛП: j(X)=C¢X®min, Ax=B, X³0. Однако эта задача имеет специальный вид. Каждый столбец матрицы A основных ограничений соответствует пути из некоторого пункта Ai в пункт Aj. Обозначим этот столбец через Aij. Из (3.9) видим, что у столбца Aij на I-м месте стоит 1, на J-м -1, а остальные элементы столбцов нулевые. Эта специфика позволяет модифицировать симплекс-метод.
Пример 3.2. Рассмотрим задачу (3.9). На рис. 3.5 изображено графическое представление этой задачи. Построим начальный базисный сетевой поток по методу проб и ошибок. Начинаем с узла 1. Полагаем: X15=A1=10, X52=10, X26=X52+A2=15, X64=7, X63=7. Поскольку узлов M, а количество отмеченных дуг M-1=5, причем из них нельзя построить ни одного цикла, полагая Xij=0 для остальных дуг, получаем базисный сетевой поток (рис. 3.5).
Найдем потенциалы узлов. Для этого полагаем U6=0 (узлу 6 инцидентны три дуги). Остальные потенциалы определяются однозначно (все потенциалы записываем рядом с узлами). Подсчитываем оценки небазисных дуг. Их значения на рисунке будем помещать под дугами или справа от них.
Поскольку имеются отрицательные оценки, построенный базисный сетевой поток не оптимален. Выбираем небазисную дугу с минимальной оценкой. Таковой является дуга (I0, J0)=(5, 3). На рис. 3.5 она отмечена двойной стрелкой. Добавление этой дуги к базисному множеству образует цикл {5, 3, 6, 2, 5}. В направлении 5®3 движения вдоль цикла дуги (6, 3), (2, 6), (5, 2) обратные. Определяем q0=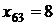
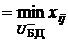 . Таким образом, (I*, J*)=(6, 3). Из базисного множества удаляем дугу (6, 3), заменив ее дугой (5, 3). Новый базисный поток будет иметь вид:
. Таким образом, (I*, J*)=(6, 3). Из базисного множества удаляем дугу (6, 3), заменив ее дугой (5, 3). Новый базисный поток будет иметь вид: 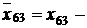 Q0=0,
Q0=0, 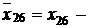 Q0=7,
Q0=7, 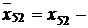 Q0=2,
Q0=2, 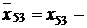 Q0=8. Остальные дуговые потоки не меняются.
Q0=8. Остальные дуговые потоки не меняются.
Дальнейшее решение задачи представлено на рис. 3.6—3.7.
Поскольку на рис. 3.7 все оценки неотрицательны, то полученный сетевой поток оптимальный. Таким образом, товар от первого поставщика будет отправлен третьему потребителю в объеме 8 Ед. по пути 1®5®3, а четвертому в объеме 2 ед. по пути 1®2®6®4. Весь товар от второго поставщика отправляется четвертому потребителю по пути 2®6®4. При этом минимальные суммарные издержки на доставку товара от поставщиков потребителям равна
J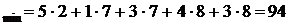 (Д. е.).
(Д. е.).
Пример 3.3. Рассмотрим задачу примера 3.1., в которой будем считать, что в пункте A4 требуется только 4 Ед. товара. Тогда модель становится открытой, поскольку спрос равен 12 Ед., а предложение 15 Ед.
Введем дополнительный 7-й узел (сток, поскольку превышает спрос) с объемом спроса, равным 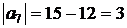 Ед., и соединим этот узел с первым и вторым узлами (источниками) дугами (1, 7), (2, 7) и стоимостью единичных потоков C17=C27=0. На рис. 3.8 изображена эта сеть. На этом же рисунке изображен и начальный базисный поток, который тоже построен методом проб и ошибок. Начинаем с узла 1. По дуге (1, 7) отправляем только 3 Ед., поскольку в этом узле требуется 3 Ед. и из узла не выходят дуги, т. е. X17=3. Оставшийся товар в объеме 7 Ед. направляем по дуге (1, 5), т. е. X15=7, далее по дуге (5, 2), т. е. X52=7. В узле 2 становится 5+7=12 Ед., но этот товар не отправляем в узел 7, поскольку в нем уже имеется 3 Ед., необходимые в этом узле.
Ед., и соединим этот узел с первым и вторым узлами (источниками) дугами (1, 7), (2, 7) и стоимостью единичных потоков C17=C27=0. На рис. 3.8 изображена эта сеть. На этом же рисунке изображен и начальный базисный поток, который тоже построен методом проб и ошибок. Начинаем с узла 1. По дуге (1, 7) отправляем только 3 Ед., поскольку в этом узле требуется 3 Ед. и из узла не выходят дуги, т. е. X17=3. Оставшийся товар в объеме 7 Ед. направляем по дуге (1, 5), т. е. X15=7, далее по дуге (5, 2), т. е. X52=7. В узле 2 становится 5+7=12 Ед., но этот товар не отправляем в узел 7, поскольку в нем уже имеется 3 Ед., необходимые в этом узле.
Далее поступаем как в примере 3.2.
На рис. 3.9 представлен оптимальный план.
Величина X17=3 означает, что в пункте A1 остается не реализованным товар в объеме 3 Ед. Из пункта A1 товар в объеме 7 Ед. отправляется в пункт A3 по пути 1®5®3. Из пункта A2 товар распределяется по двум направлениям: в пункт A3 1 Ед. по пути 2®3 и в пункт A4 4 Ед. по пути 2®6®4. Минимальные издержки на перевозку товара равны j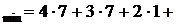
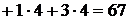 (Д. е.).
(Д. е.).
Пример 3.4. Рассмотрим задачу примера 3.3. В оптимальном сетевом потоке (см. рис. 3.9) имеются две нулевые небазисные оценки: D12=0, D34=0. Поток невырожденный. Поэтому можем утверждать, что оптимальный сетевой поток неединственный. Легко видеть, что, например, потоки, изображенные на рис. 3.11, 3.12, тоже оптимальные. Заметим, что для этой же задачи существуют и другие оптимальные сетевые потоки.