МЕТОДИЧНІ ВКАЗІВКИ З ВИКОНАННЯ КУРСОВОЇ ТА ДИПЛОМНОЇ РОБІТ

У практиці лісівничих, біологічних і екологічних досліджень часто буває необхідним перевірити ту чи іншу гіпотезу, тобто з'ясувати, наскільки одержаний експериментальний матеріал підтверджує теоретичні припущення, наскільки аналізовані дані співпадають з теоретично очікуваними. Виникає завдання статистичної оцінки різниці між фактичними даними і теоретичним очікуванням, встановлення того, в яких випадках І з яким ступенем ймовірності можна вважати цю різницю вірогідною, і, навпаки, коли її варто вважати несуттєвою, незначною, тобто такою, що перебуває в межах випадковості. В останньому разі зберігається гіпотеза, виходячи з якої було обраховано теоретично очікувані дані, або показники.

Розрахунок частот теоретичних розподілів. Досить велику сукупність часто можна представити у вигляді емпіричної кривої розподілу. Майже кожний емпіричний розподіл можна, в свою чергу, інтерпретувати якимсь теоретичним типом розподілу, що, як правило, розкриває нові особливості вивченого явища та дозволяє прогнозувати деякі його властивості. Принципи побудови статистичних розподілів і інші подробиці щодо них можна знайти в курсах з теорії ймовірностей.

В залежності від характеру змін випадкових величин, які входять до розподілу, розрізняють два основних типи розподілів: дискретні та неперервні. Розподілами дискретного типу є: альтернативний, біноміальний, мультіноміальний; а неперервного - показовий, Максвела, Релея, Парето тощо. Передує тим і іншим типам нормальний розподіл неперервного типу, який є основним, адже, згідно з теорією ймовірностей, до нього кінець кінцем прямують всі відомі типи розподілів. Ми розглянемо лише деякі з цих типів розподілів.

Визначення теоретичних частот емпіричного ряду за тим чи іншим законом розподілу ймовірностей є процес вирівнювання емпіричного розподілу, звільнення його вад усього випадкового, з тим щоби виявити основну тенденцію варіювання тієї чи іншої ознаки, закон її розподілу.

Нормальний Розподіл широко розповсюджений, має найбільше значення для теорії та практики біометричних досліджень, тому в першу чергу порівнюють одержаний емпіричний розподіл з нормальним, теоретичні частоти якого необхідно для цього обрахувати, що можна зробити за формулою:

,

Де ft - теоретичні частоти нормальної кривої; N - об'єм виборки; с - класовий інтервал; 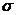- середнє квадратичне відхилення; Е - основа натуральних логарифмів, дорівнює 2,7182818; - нормоване відхилення; 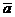- середня арифметична; АІ - варіанси (середини класів) ряду.

Біноміальний розподіл. Група об'єктів може характеризуватись не лише кількісними ознаками, які матимуть різний ступень свого виявлення та вимірюються іменованими величинами (в кілограмах, сантиметрах, літрах та інших одиницях вимірювання). Є ознаки, які звичайно не мають градацій (жіноча чи чоловіча стать, забарвлення горошин і т. ін.). У кожного об'єкта така ознака може бути, а може й не бути. Такі ознаки називаються якісними, або альтернативними, Принципіальної різниці між кількісними та якісними ознаками немає. У більшості ознак, які вважаються якісними, при більш ретельному вивченні може бути знайдено спосіб вимірювання ступеня прояву ознаки, і тоді якісна ознака стане кількісною.

Характеристика групи за якісною ознакою полягає в тому, що вказується, скільком особинам у цій групі притаманна ця ознака, і скільком ні. Для такої характеристики використовуються такі означення:

N - загальна кількість особин у групі (наприклад, 300);

N+ - кількість особин, яким притаманна дана ознака (100);

N– - кількість особин, у яких дана ознака відсутня (200);

- частка особин з наявною ознакою (100/300 = 0,33);

- частка особин з відсутністю ознаки (200/300 = 0,67).

Очевидні наступні рівності;

N+ + n– = n, p + q = 1, q = 1 – p.

Якщо вивчається кілька (r) груп, однакових за кількістю особин, що входять до них (п), то можна скласти розподіл таких груп за числом особин, яким притаманна вивчена ознака.

Наприклад, 200 горошинок, серед яких були зелені та жовті, випадковим чином розподілили на десятки (20 десяток). У кожній десятці може зустрітись 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 і навіть 10 зелених горошин. Кілька десяток будуть виключно жовтими, кілька — матимуть по 1 зеленій горошині, кілька - по 2 і т. д.

Такий розподіл випадкових рівночисельних груп за значенням n+ (за числам об'єктів з вивченою ознакою у кожній групі) називається біноміальним (рис. 7).

Рис. 7. Емпіричні (1) та теоретичні (2) частоти (f) біноміального розподілу; х – варіанти

Назва пояснюється, по-перше, тим, що ознака може мати лише два варіанти (є — немає), по-друге, закономірності таких розподілів мають кількісне вираження, пов'язане з коефіцієнтами розкладення бінома Ньютона. Але ми для розрахунку частостей біноміального розподілу скористаємось так званою рекурентною[6] формулою;

Де - наступна частість; П -Об'єм проби; Р, q - частка присутності та відсутності вивченої ознаки в сукупності, - попередня частість; i - номер члена ряду частостей.

Початковий член ряду частостей визначається за формулою:

.

Майте на увазі, що рекурентні формули вимагають достатньої точності розрахунків, адже всі наступні результати обрахунків грунтуються на попередніх, і навіть невелика помилка, припущена на початку, швидко збільшується наприкінці ряду.

Розподіл рідкісних подій (закон Пуасона). Характер біноміальної кривої визначається двома величинами; числом випробувань i ймовірністю очікуваного результата. При Р = 0,5 біноміальна крива симетричяа і в міру зростання кількості випробувань набуває плавного ходу на всьому протязі. Якщо РQ , біноміальна крива стає асиметричною (особливо із збільшенням різниці між Р та Q). Коли ймовірність очікуваної події обчислюється сотими і тисячними частками одиниці, розподіл частоти такого рідкісного явища в П незалежних випробуваннях виявляється вкрай асиметричним. Розподіл частоти таких рідкісних подій описується формулою Пуасона:

де Т - частота очікуваної події в П незалежних випробуваннях; АПр — найбільш ймовірна частота рідкісної події; Е = 2,7183... — основа натуральних логарифмів; Т! - факторіал частоти, або добуток натуральних чисел 1·2·3 ... Т.

Для того, щоб формула Пуасона представляла не ймовірності, а очікувані абсолютні частоти (р') рідкісної події, зазначеній формулі надають наступного виразу:

.

У цьому разі Р’ – теоретичні ординати кривої розподілу Пуасона, або очікуване число випадків рідкісної події в кожному окремо взятому класі випробування (0, 1, 2, 3, 4 і т. д.); П - кількість випробувань; - середня кількість випадків, які фактично спостерігались (береться замість А); пояснення інших символів такі ж самі, що і в попередній формулі.