МЕТОДИЧЕСКИЕ УКАЗАНИЯ По выполнению лабораторно-практических занятий и заданий для самостоятельных работ по дисциплине «Физическая и коллоидная химия»
Страница 6 из 11
Пользуясь уравнением Гиббса, по изотерме поверхностного натяжения σ = f(c) можно построить соответствующую изотерму адсорбции, пользуясь несложными графическими приемами (рис. 2.2).
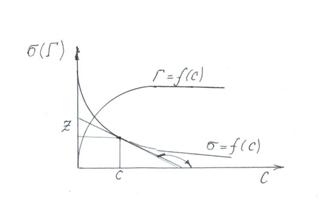
Рис. 2.2. Изотермы поверхностного натяжения и адсорбции на границе раздела жидкость – газ.
К произвольно выбранным точкам на экспериментально полученной кривой σ = f(c) проводят касательные и продолжают до пересечения с осью ординат. Тогда 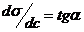 , а по построению
, а по построению 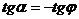 .
. 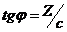 , откуда
, откуда 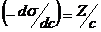 и Г = Z/RT. Рассчитав величины адсорбции для ряда концентраций, строят изотерму адсорбции.
и Г = Z/RT. Рассчитав величины адсорбции для ряда концентраций, строят изотерму адсорбции.
При очень малых концентрациях ПАВ уменьшение поверхностного натяжения прямо пропорционально концентрации:
σо – σ = k с (2.2),
Где σо и σ - поверхностное натяжение чистого растворителя и раствора, k - константа, служащая мерой адсорбционной активности растворенного вещества.
При больших концентрациях ПАВ Падение поверхностного натяжения с ростом концентрации хорошо описывается эмпирическим уравнением Б. А.Шишковского, полученного для водных растворов жирных кислот до С8.
σо – σ = σо В ln (c/A + 1) (2.3),
Где В – безразмерная константа, примерно одинаковая для всех членов выбранного гомологического ряда ПАВ, обладающих одинаковыми функциональными группами (для жирных кислот В = 0,2), 1/А – константа, которая при заданной температуре зависит от длины углеводородного радикала и увеличивается в 3 – 3,5 раза при увеличении цепи на -СН2- группу; она называется удельной капиллярной постоянной.
Иной подход к выводу уравнения адсорбции был предложен в 1917 году Ленгмюром. В основе его лежат молекулярно - кинетические соображения, позволяющие придать четкий физический смысл всем константам уравнения. Рассмотрим 1 см2 поверхностного слоя, находящегося в равновесии с бифункциональным жидким раствором ПАВ и с газовой фазой (воздух или насыщенный пар). Пусть молекула ПАВ занимает в поверхностном слое площадь so, а число молекул на 1 см2 равно γ. γ = Гs×NA, где Гs – число молей ПАВ на поверхности 1 см2 , NA – постоянная Авогадро. В разбавленных растворах при отсутствии адсорбции можно принять, что Гs=Г (Г – число молей ПАВ в любом поперечном срезе объема раствора), тогда
γ = Г×NA (2.4)
Доля площади, занятой молекулами ПАВ, составляет so γ, а доля свободной поверхности, занятой молекулами растворителя (1 - so γ). Скорость адсорбции, то есть перехода ПАВ из объема раствора в поверхностный слой, пропорциональна доле свободной поверхности и концентрации молекул в растворе:
V1 = k1×c (1 - so γ) (2.5)
Скорость обратного процесса – десорбции, пропорциональна доле занятой площади:
V2 = k2×(so γ) (2.6),
Где k1 и k2 – константы прямого и обратного процессов.
В состоянии равновесия скорости равны. Приравняв (2.5) и (2.6), получим:
K1/ k2 = К = 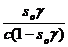 (2.7)
(2.7)
Решая уравнение относительно числа молекул в поверхностном слое γ, получим:
γ = 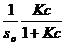 (2.8)
(2.8)
По физическому смыслу доля занятой поверхности при насыщении достигает единицы, so γ∞ = 1, следовательно,
1/ so = γ∞= Г ∞ ×NA (2.9)
Подставляя (2.9) и (2.4) в (2.8), получим:
Г = Г ∞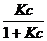 (2.10)
(2.10)
Это и есть уравнение Ленгмюра, которое содержит константы с ясным физическим смыслом: К – константа равновесия сорбционного процесса, выраженная через отношение констант скоростей адсорбции и десорбции. Г ∞ - Предельная адсорбция, отвечающая полному насыщению поверхностного слоя молекулами ПАВ – это так называемый «частокол Ленгмюра» (рис. 2.1. б)