Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Страница 8 из 9
78. Некоторые типы случайных процессов. Процесс Бернулли.
1). Процесс Бернулли – это процесс с непрерывными пространствами параметров и состояний.
2). Пусть 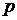 и
и 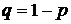 – соответственно вероятности появления успеха или неуспеха в каждом испытании. Обозначим
– соответственно вероятности появления успеха или неуспеха в каждом испытании. Обозначим  – количество успехов в
– количество успехов в 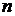 испытаниях. Ясно что
испытаниях. Ясно что 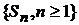 – случайный процесс с пространством состояний
– случайный процесс с пространством состояний 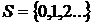 , одномерное распределение вероятностей которого для данного
, одномерное распределение вероятностей которого для данного 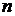 определяется как:
определяется как: 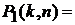
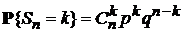 ,
, 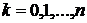 . Процесс
. Процесс  , определяемый согласно (13), называется процессом Бернулли.
, определяемый согласно (13), называется процессом Бернулли.
3). Процесс Бернулли обладает свойством: в любом конечном промежутке времени с положительной вероятностью может появиться сколь угодно большое число заявок.
4). 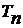 – длина дискретного интервала времени между двумя последовательными успехами в случайном процессе Бернулли. Тогда:
– длина дискретного интервала времени между двумя последовательными успехами в случайном процессе Бернулли. Тогда: 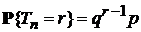 ,
, 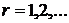 , и при этом случайные величины
, и при этом случайные величины 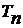 линейно зависимы и одинаково распределены.
линейно зависимы и одинаково распределены.
5). Процесс Бернулли – это процесс восстановления с дискретным временем. Кроме того, процесс Бернулли является процессом с независимыми приращениями. Отсюда следует, что он не является марковским.
79. Некоторые типы случайных процессов. Процесс Бернулли.
1). Процесс Бернулли является процессом с линейно связанными приращениями.
2). Процесс Бернулли не обладает марковским свойством.
3). Моментные характеристи процесса Бернулли имеют вид: 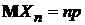 ,
, 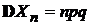 ,
, 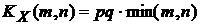 .
.
4). Процесс Бернулли не является процессом восстановления.
5). Невозможно определить процесс Бернулли для случая непрерывного времени.
80. Некоторые типы случайных процессов. Процесс Пуассона.
1). Моментные характеристики процесса Пуассона имеют вид: 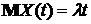 ,
, 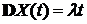 ,
,  .
.
2). Процесс Пуассона 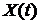 является процессом с дискретным пространством состояний
является процессом с дискретным пространством состояний  И дискретным временем.
И дискретным временем.
3). Промежутки времени между двумя последовательными появлениями событиями в пуассоновском процессе суть н. о.р. с. в. с постоянной плотностью распределения.
4). Пуассоновский процесс не является процессом восстановления.
5). Пуассоновский процесс в силу независимости приращений, не обладает марковским свойством.
81. Простой пуассоновский процесс (простейший поток событий).
1). Отсутствие последействия: для любого конечного набора непересекающихся полуинтервалов времени 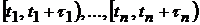 число событий в них K1, …, Kn – функционально зависимые в совокупности случайные величины.
число событий в них K1, …, Kn – функционально зависимые в совокупности случайные величины.
2). Стационарность: вероятность Pt, t+t(K) появления ровно K событий в интервале времени 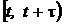 является функциональной зависимостью только от времени T, т. е. от его положения на оси времени:
является функциональной зависимостью только от времени T, т. е. от его положения на оси времени: 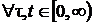 Pt, t+τ(K) = F(Pt(K)), K = 0, 1, 2,…
Pt, t+τ(K) = F(Pt(K)), K = 0, 1, 2,…
3). Ординарность: вероятность появления более одного события в интервале времени длиною T – величина, отличная на бесконечно малую относительно T от вероятности достоверного события.
4). Случайный процесс, отвечающий условиям стационарности, отсутствия последействия и ординарности, носит название простейшего потока событий или простого пуассоновского процесса.
5). Моментная функция математического ожидания пуассоновского процесса 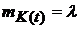 и не зависит от времени.
и не зависит от времени.
82. Пуассоновский процесс с переменной интенсивностью.
1). Функция математического ожидания:  .
.
2). Корреляционная функция случайного процесса: 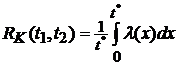 , где
, где 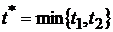 .
.
3). Отказ от условия стационарности приводит к моделям пуассоновского процесса с переменной интенсивностью. Для такого точечного процесса 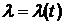 — известная (неслучайная) функция времени, TÎ[0,¥).
— известная (неслучайная) функция времени, TÎ[0,¥).
4). Если интенсивность потока событий задана неслучайной интегрируемой функцией L(T) и поток отвечает условиям отсутствия последействия и ординарности, то он теряет свойства пуассоновского процесса.
5). Даже, если интенсивность 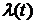 сама является случайной функцией, например (в самом простом случае) интенсивность
сама является случайной функцией, например (в самом простом случае) интенсивность 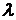 — случайная величина, принимающая одно из двух значений:
— случайная величина, принимающая одно из двух значений: 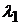 с вероятностью P или
с вероятностью P или 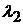 с вероятностью Q = 1 – P, процесс остается быть пуассоновским.
с вероятностью Q = 1 – P, процесс остается быть пуассоновским.
83. Сложный пуассоновский процесс.
1). Введение в модель веса событий нетрудно осуществить, когда этот вес V является детерминированной величиной и одинаков для всех событий. В этом случае простой пуассоновский процесс превращается в взвешенный пуассоновский процесс Q(T), выражающий суммарный вес событий, происходящих за интервал времени [0, T), и принимающий значения, кратные V: Q(T) = V K(T).
2). Функция математического ожидания взвешенного пуассоновского процесса: MQ(T) = mK(T).
3). Корреляционная функция взвешенного пуассоновского процесса: RQ(T1,T2) = RK(T1,T2).
4). Сложный пуассоновский процесс представляет собой сумму неслучайного числа K(T) случайных величин Vi с равномерными распределениями и определяется равенством: 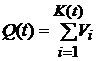 .
.
5). Сложный пуассоновский процесс представляет собой сумму неслучайного числа K(T) случайных величин Vi с равномерными распределениями и определяется как линейная комбинация: 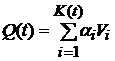 , где
, где 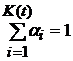 .
.
84. Некоторые типы случайных процессов. Процесс Гаусса.
1). Гауссовский процесс – это вещественный случайный процесс 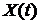 ,
, 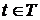 , любые конечномерные распределения
, любые конечномерные распределения 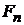 которого являются гауссовскими, т. е. при любых
которого являются гауссовскими, т. е. при любых 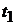 ,
,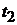 ,...,
,...,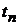
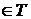 совместное распределение с. в.
совместное распределение с. в. 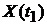 ,
, 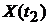 ,...,
,...,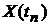 имеет вид
имеет вид
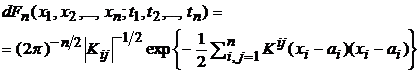 ,
,
Где 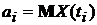 ,
, 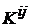 – матрица, обратная к
– матрица, обратная к 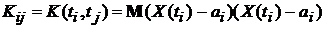 .
.
2). Гауссовский процесс – это процесс с дискретными пространством состояний 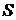 и пространством параметров
и пространством параметров 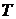 .
.
3). Случайный процесс 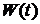 , является винеровским процессом, если это неоднородный гауссовский процесс с независимыми приращениями, для которого
, является винеровским процессом, если это неоднородный гауссовский процесс с независимыми приращениями, для которого 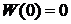 и
и 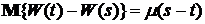 ,
, 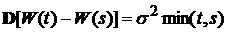 .
.
4). Виннеровский процесс 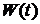 не имеет стационарных независимых приращений.
не имеет стационарных независимых приращений.
5). Для любого заданного интервала 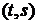 с. в.
с. в. 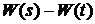 распределена со средним
распределена со средним 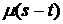 и постоянной дисперсией. Величина
и постоянной дисперсией. Величина 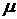 называется коэффициентом сноса (дрейфа) процесса
называется коэффициентом сноса (дрейфа) процесса 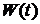 .
.
85. Стандартный винеровский процесс или процесс броуовского движения.
1). Приращения 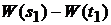 и
и 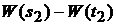 винеровского процесса
винеровского процесса 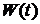 на любых непересекающихся интервалах времени
на любых непересекающихся интервалах времени 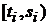 ,
, 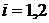 , являются линейно связанными.
, являются линейно связанными.
2). Если 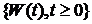 – стандартный винеровский процесс, – процесс
– стандартный винеровский процесс, – процесс 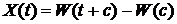 ,
, 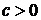 не является винеровским.
не является винеровским.
3). Стандартным винеровским процессом, или процессом броуовского движения, называется гауссовский случайный процесс 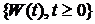 с непрерывным временем, моментными характеристиками
с непрерывным временем, моментными характеристиками 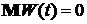 ,
, 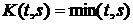 ,
, 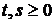 , и выходящий из нуля, т. е.
, и выходящий из нуля, т. е. 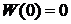 .
.
4). Если 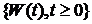 – стандартный винеровский процесс, – процесс
– стандартный винеровский процесс, – процесс 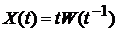 ,
, 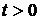 ,
, 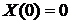 не является винеровским.
не является винеровским.
5). Если 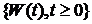 – стандартный винеровский процесс, – процесс
– стандартный винеровский процесс, – процесс 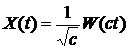 , где
, где 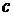 – любая положительная константа, не является винеровским.
– любая положительная константа, не является винеровским.
ПП 2.8.Элементы теории надежности.
86. Определение надежности.
1). Надежность (Reliability) есть вероятность того, что система выполняет свои функции в соответствии с предъявляемыми требованиями в течение заданного интервала времени.
2). Обычно с понятием надежности связывается определенная вероятность того, что в фиксированные моменты времени 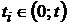 , система работает нормально.
, система работает нормально.
3). Надежность – это количественный показатель, а не свойство.
4). Предположим, что состояние системы в момент времени  описывается случайным вектором
описывается случайным вектором 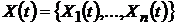 . Тогда вероятность
. Тогда вероятность  – есть надежность системы.
– есть надежность системы.
5). Если не производятся ремонты или замены отказавших элементов системы, то этого не достаточно, что бы говорить, что состояние системы в произвольный момент времени  описывает поведение системы на всем интервале времени
описывает поведение системы на всем интервале времени 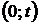 .
.
87. Мгновенная и интервальная готовности системы.
1). Предельная интервальная готовность – это математическое ожидание доли времени нормального функционирования на конечном интервале времени.
2). Интервальная готовность (interval availability) – математическое ожидание доли времени нормального функционирования системы в произвольные фиксированные моменты времени в течение заданного интервала времени.
3). Мгновенная готовность (pointwise availability) – математическое ожидание доли времени нормального функционирования системы в течение заданного интервала времени.
4). Предельная интервальная готовность – это коэффициент  , где
, где 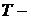 Среднее время безотказного функционирования системы, а
Среднее время безотказного функционирования системы, а 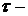 Среднее время ремонта.
Среднее время ремонта.
5). Предельная интервальная готовность и предельная интервальная надежность – это тождественные понятия.
88. Распределения времени безотказной работы. Дискретные распределения.
1). Среди дискретных распределений в теории надежности одним из основных является так называемое отрицательное биномиальное распределение Паскаля:
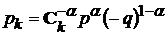 ,
, 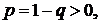
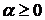 ,
, 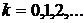
2). Для любой системы интенсивности отказов не могут быть описаны биномиальным распределением:
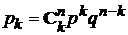 ,
,
Где 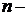 Положительные числа,
Положительные числа, 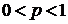 ,
, 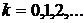
3). Для описания распределений времени безотказной работы используются: плотность вероятности 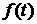 (когда она существует), функция распределения
(когда она существует), функция распределения 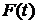 и интенсивность отказов
и интенсивность отказов 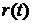 .
.
4). Отрицательное биномиальное распределение Паскаля имеет возрастающую интенсивность отказов при 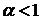 .
.
5). Распределение Пуассона
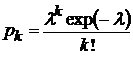 ,
,  ,
, 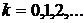
Всегда показывает снижающуюся тенденцию интенсивности отказов.
89. Распределения времени безотказной работы. Непрерывные распределения.
1). Для описания отказов элементов различных систем не используются непрерывные распределения.
2). Непрерывным аналогом дискретного распределения отказов Пуассона является экспоненциальное распределение:
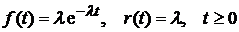 .
.
3). Модифицированное распределение экстремального значения:
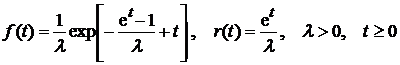
Имеет убывающую интенсивность отказов.
4). Усеченное нормальное распределение:
 ,
,
Где 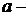 Нормирующая константа, – имеет убывающую интенсивность отказов.
Нормирующая константа, – имеет убывающую интенсивность отказов.
5). Логарифмически-нормальное распределение
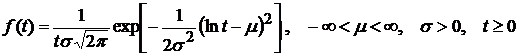
Имеет возрастающую интенсивность отказов в сравнительно широком диапазоне.