Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

ПП 2.1. Случайные процессы. Основные понятия и определения. Классификация случайных процессов.

1. Случайные процессы. Основные понятия и определения.

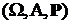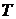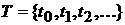Заданы: полное вероятностное пространство и произвольное множество вида или 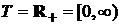. Рассмотрим измеримое отображение 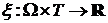, индуцирующее вероятностное пространство 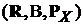, где 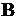– 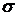-алгебра борелевских множеств из 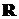, – вероятность, заданная на 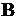. Случайным процессом называется:

1). Отображение .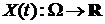

2). Отображение .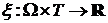

3). При фиксированном значении элементарного исхода 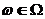отображение 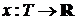является случайной функцией 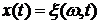времени .

4). При фиксированном значении времени 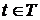отображение 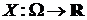не является случайной величиной .

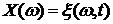5). Параметр 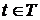называют дискретным временем.

2. Функция распределения случайного процесса.

1). Функция распределения 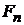распадается в произведение одномерных функций распределений соответствующих случайных величин .

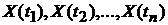2). Функция распределения 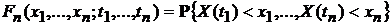, , 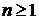называется 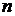-мерным распределением случайного процесса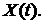

3). Функция распределения 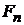представляет собой вектор-функцию, компонентами которой являются одномерные функции распределений соответствующих случайных величин .

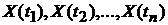4). Семейство 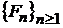конечномерных распределений случайного процесса 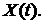образует выборочное пространство .

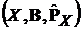5). Случайный процесс детерминирован и для него не определена функция распределения.

3. Теорема Колмогорова.

1). Условие симметрии: для любых перестановок индексов 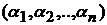выполняется равенство 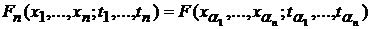для функции распределения случайного процесса не имеет места.

2). Условие согласованности для случайных процессов имеет вид: , .

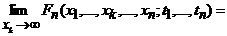
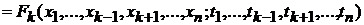3). Некоторое семейство конечномерных распределений 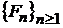определяет некоторый случайный процесс тогда и только тогда, когда это семейство удовлетворяет условиям симметрии и согласованности.

4). Семейство конечномерных распределений случайного процесса 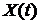вероятностную меру 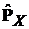, заданную на выборочном пространстве этого случайного процесса определяет неоднозначно.

5). Семейство распределений любого случайного процесса 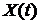не является конечномерным.

4. Классификация случайных процессов.

1). Если 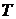состоит из счетного числа изолированных точек, то соответствующий случайный процесс 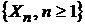называют временным рядом, или случайным процессом с дискретным временем.

2). Случайный процесс 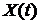является дискретным, если дискретно его пространство состояний, при этом множество 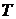– может быть интервалом из .

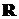3). Совокупность 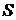всех возможных значений дискретного случайного процесса называется его пространством состояний, а для непрерывного случайного процесса – фазовым пространством.

4). Для дискретных случайных процессов и множество 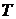и пространство состояний – дискретны.

5). Для непрерывных случайных процессов и множество 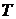и пространство состояний – непрерывны.

5. Пуассоновский случайный процесс.

1). Если вероятность 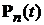числа событий на интервале 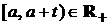зависит только от 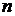и не зависит от положения интервала на временной оси, то такой случайный процесс обладает свойством стационарности.

2). Если события, происходящие на непересекающихся интервалах времени суть независимые случайные величины, то такой случайный процесс обладает свойством отсутствия последствия.

3). Если вероятность того, что в малом интервале времени 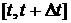произойдет не более одного события, есть величина бесконечно малая порядка 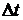при 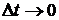, то случайный процесс обладает свойством ординарности.

4). Поток событий 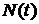, удовлетворяющий условиям: стационарности, отсутствия последействия и ординарности называется пуассоновским, или простейшим.

5). Пуассоновский процесс является непрерывным процессом с дискретным временем.

6. Пуассоновский случайный процесс.

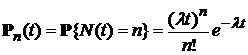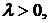
1). Простейший поток событий описывается одномерным распределением , 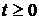. Параметр называется интенсивностью пуассоновского потока событий.

2). Простейший поток событий описывается многомерным распределением и характеризуется интенсивностью .

3). Пусть 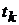(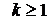, 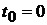) – моменты появления пуассоновских событий. Тогда случайные величины 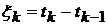независимы в совокупности и .

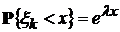4). Все траектории 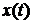пуассоновского процесса представляют собой непрерывные монотонные функции.

5). Траектории 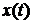пуассоновского процесса могут содержать конечное множество точек разрыва второго рода.

7. Моментные функции случайных процессов. Функция математического ожидания.

1). Функцией математического ожидания (м. о.) 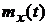дискретного случайного процесса X(T) называется функция, которая для каждого значения аргумента T равна математическому ожиданию сечения процесса X(T) при данном значении аргумента, т. е.

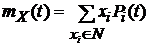
И, в отличии от функции математического ожидания непрерывного процесса имеет случайный характер.

2). Функцией математического ожидания (м. о.) 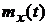непрерывного случайного процесса X(T) называется неслучайная функция, которая для каждого значения аргумента T равна математическому ожиданию сечения процесса X(T) при данном значении аргумента, т. е.

.

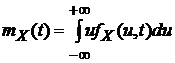3). Для дискретного случайного процесса X(T) с бесконечным или счетным множеством реализаций, функция математического ожидания не существует.

4). Свойства случайного процесса могут характеризоваться с той или иной полнотой так называемыми моментными функциями, которые принципиально отличны от понятия моментов случайных величин.

5). К основным моментным функциям случайных процессов относятся функции математического ожидания, дисперсии и среднего квадратического отклонения.

8. Моментные функции случайных процессов. Функция дисперсии.

1). Функцией дисперсии дискретного случайного процесса X(T) называется неслучайная функция, которая для каждого значения аргумента T равна дисперсии сечения процесса при данном значении аргумента, т. е.

.

2). Функцией дисперсии непрерывного случайного процесса X(T) называется неслучайная функция, которая для каждого значения аргумента T равна дисперсии сечения процесса при данном значении аргумента, т. е.

.

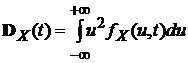3). И для дискретных, и для непрерывных случайных процессов, функция дисперсии является случайной величиной.

4). Вместо функции дисперсии функция среднего квадратичного отклонения (стандартного отклонения) 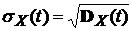не используется, так как для случайных процессов не имеет смысла.

5). Обе функции: дисперсия и стандартное отклонение, не могут характеризуют собой полные вариации случайного процесса относительно среднего значения случайного процесса в силу своей случайной природы.

9. Корреляционная функция случайного процесса.

1). Для определения корреляционной функции непрерывного случайного процесса, необходимо случайный процесс дискретизировать и воспользоваться соотношением:

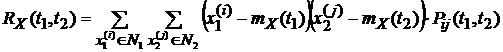
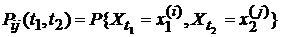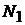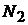(здесь , и – множества значени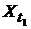й и 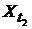в соответствующих точках дискретизации.

2). Из общего определения корреляционной функции следует, что для каждой пары различных сечений случайного процесса значение корреляционной функции равно смешанному центральному моменту первого порядка этих сечений.

3). Нормированный аналог 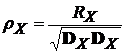для корреляционной функции случайного процесса (непрерывного или дискретного) не имеет смысла.

4). Корреляционной функцией (к. ф.) 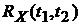дискретного случайного процесса X(T) называется неслучайная функция, которая для каждой пары значений аргументов T1 и T2 равна корреляционному моменту сечений процесса 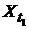и 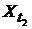, соответствующих этим значениям аргументов, т. е.

.

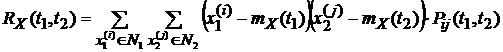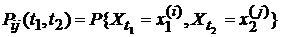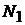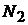(здесь , и – множества значений сечени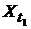й и .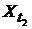

5). Из неравенства Коши-Буняковского следует, что:

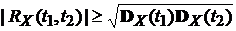
И следовательно нормированная корреляционная функция всегда .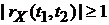

• < Назад
• Вперёд >