ЗАДАНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ ПО МЕТОДАМ ОПТИМИЗАЦИИ И ПРИНЯТИЮ РЕШЕНИЙ
ЗАДАНИЯ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ ПО МЕТОДАМ ОПТИМИЗАЦИИ И ПРИНЯТИЮ РЕШЕНИЙ
МЕТОДЫ ПОИСКА ЭКСТРЕМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
БЕЗУСЛОВНАЯ ОПТИМИЗАЦИЯ
ЗАДАНИЕ 1. Дана функция:
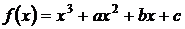 .
.
В области определения найти ее минимум.
1. Находя производную 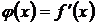 и решая уравнение
и решая уравнение 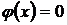
А). методом половинного деления;
Б). методом хорд;
В). методом касательных (Ньютона).
Точность вычислений 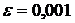 .
.
2. Не производя дифференцирования функции 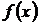 , организовать процедуры:
, организовать процедуры:
А). методом половинного деления;
Б). методом золотого сечения.
Точность вычислений 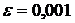 .
.
Коэффициенты 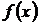 по вариантам заданий приведены в в таблице:
по вариантам заданий приведены в в таблице:
|
№ Варианта
|
|
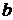
|

|
|
1
|
2
|
3
|
-1
|
|
2
|
3
|
-2
|
4
|
|
3
|
1
|
-1
|
8
|
|
4
|
5
|
3
|
2
|
|
5
|
2
|
4
|
-1
|
|
6
|
3
|
2
|
4
|
|
7
|
4
|
-3
|
2
|
|
8
|
6
|
4
|
7
|
|
9
|
2
|
8
|
-3
|
|
10
|
3
|
-5
|
6
|
МЕТОД ГРАДИЕНТНОГО СПУСКА ПОИСКА МИНИМУМА ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
ЗАДАНИЕ 2. Пусть требуется найти локальный минимум функции
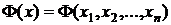 .
.
Выберем начальное приближение 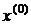 и построим последовательность
и построим последовательность 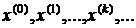 , в которой каждое очередное приближение
, в которой каждое очередное приближение 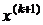 получается из предыдущего
получается из предыдущего 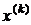 "шагом" в направлении вектора
"шагом" в направлении вектора 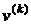 :
:
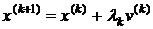 . (1)
. (1)
Выбор вектора 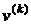 определяет различные варианты метода "спуска" к минимуму
определяет различные варианты метода "спуска" к минимуму 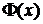 .
.
Величина шага управляется выбором 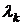 . Обычно
. Обычно 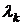 выбирается так, чтобы функция
выбирается так, чтобы функция
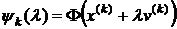 (2)
(2)
Принимала наименьшее значение.
Точность полученного приближения к минимуму обычно оценивается по величине отклонения двух соседних приближений 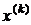 и
и 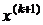 , например
, например
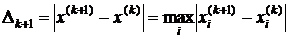 (3)
(3)
Или
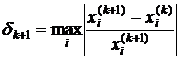 . (3.1)
. (3.1)
Процесс приближений прекращается, если 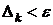 (абсолютная оценка приближения) или
(абсолютная оценка приближения) или 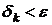 (относительная оценка приближения), где
(относительная оценка приближения), где  Заданная точность.
Заданная точность.
"Скорейший" спуск получается, если шаг делать в направлении быстрейшего убывания 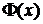 , то есть вдоль вектора
, то есть вдоль вектора
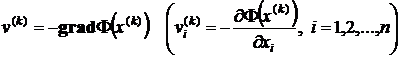 . (4)
. (4)
Так как градиент  в любой точке ортогонален к поверхности уровня
в любой точке ортогонален к поверхности уровня  , то в точке
, то в точке 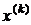 следует двигаться в направлении вектора
следует двигаться в направлении вектора 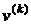 до такой точки
до такой точки 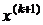 , в которой
, в которой 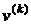 ортогонален вектору
ортогонален вектору 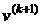 (в этой точке
(в этой точке 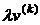 касается поверхности уровня, то есть будет достигнут минимум функции
касается поверхности уровня, то есть будет достигнут минимум функции  ).
).
Если 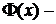 Квадратичная функция (что как раз и имеет место в задании). То непосредственный метод скорейшего спуска сходится довольно-таки медленно. Поэтому необходимо использовать модифицированный Метод сопряженных градиентов Флетчера-Ривса, который обеспечивает более быструю сходимость. В этом методе направление спуска – вектор
Квадратичная функция (что как раз и имеет место в задании). То непосредственный метод скорейшего спуска сходится довольно-таки медленно. Поэтому необходимо использовать модифицированный Метод сопряженных градиентов Флетчера-Ривса, который обеспечивает более быструю сходимость. В этом методе направление спуска – вектор 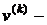 Выбирается следующим образом:
Выбирается следующим образом:
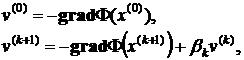
Где

Таким образом, на каждом шаге спуск несколько отклоняется от "скорейшего" в направлении предыдущего шага, что дает некоторое ускорение сходимости вблизи точки минимума, когда градиент близок к нулю.
В случае квадратичной функции 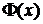 описываемые методы сходятся при любом выборе начального приближения
описываемые методы сходятся при любом выборе начального приближения 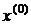 .
.
Для вычисления 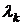 на каждом шаге спуска нужно находить минимум функции одной переменной
на каждом шаге спуска нужно находить минимум функции одной переменной  , определяемой соотношением (2).
, определяемой соотношением (2).
В общем случае для этого можно решить уравнение
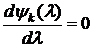 ,
,
(необходимое условие экстремума), каким-либо из приближенных методов.
В случае, если 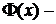 Квадратичная функция,
Квадратичная функция,  представляет собой квадратный трехчлен относительно
представляет собой квадратный трехчлен относительно 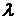 с положительным старшим коэффициентом и его минимум можно найти, если известны значения
с положительным старшим коэффициентом и его минимум можно найти, если известны значения  при каких-либо трех значениях
при каких-либо трех значениях 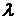 . Выберем, например для
. Выберем, например для 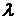 значения –1, 0, 1 и вычислим (обратившись к процедуре
значения –1, 0, 1 и вычислим (обратившись к процедуре 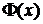 ) соответствующие значения
) соответствующие значения 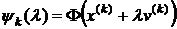 . Обозначим их через
. Обозначим их через 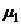 ,
, 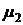 и
и  . Здесь
. Здесь 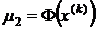 на самом деле можно не вычислять, так как оно известно с предыдущего шага. Тогда
на самом деле можно не вычислять, так как оно известно с предыдущего шага. Тогда 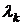 находится по формуле
находится по формуле
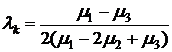 .
.
Для контроля за процессом сходимости спуска на каждом шаге удобно выдавать на печать величины:  (номер шага),
(номер шага), 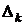 (или
(или 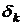 , если оценка ведется по относительной точности),
, если оценка ведется по относительной точности),  . Метод сходится к точке минимума
. Метод сходится к точке минимума 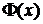 , если:
, если:
1. 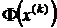 убывает;
убывает;
2. 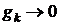 ;
;
3. 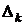 (или
(или 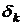 )
) 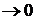 .
.
ЗАДАНИЕ 2. Найти экстремум функции
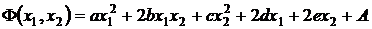 .
.
Числовые параметры функции даны в таблице для каждого варианта.
|
№ Варианта
|
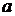
|
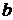
|

|
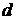
|
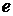
|
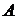
|
Начальные данные
|
Точность
|
|
I
|
-1
|
2
|
-3
|
2
|
1
|
10
|
(-1; -1)
|
0,02
|
|
II
|
-2
|
3
|
-1
|
2
|
3
|
7
|
(0; 0)
|
0,01
|
|
III
|
-3
|
3
|
-3
|
2
|
5
|
3
|
(-2; 1)
|
0,03
|
|
IV
|
-1
|
4
|
-1
|
2
|
2
|
3
|
(2; 1)
|
0,015
|
|
V
|
-2
|
4
|
-5
|
1
|
1
|
3
|
(0; 0)
|
0,01
|
|
VI
|
-3
|
3
|
-2
|
2
|
4
|
1
|
(1; 1)
|
0,01
|
|
VII
|
-1
|
3
|
-3
|
1
|
1
|
5
|
(2; -1)
|
0,02
|
|
VIII
|
-4
|
5
|
-2
|
1
|
1
|
6
|
(0; 0)
|
0,02
|
|
IX
|
-2
|
3
|
-2
|
3
|
3
|
5
|
(-1; -1)
|
0,015
|
|
X
|
-1
|
1
|
-1
|
4
|
3
|
5
|
(1; 1)
|
0,02
|
Для вычисления экстремума используйте прямой метод градиентного спуска. При вычислении точности руководствуйтесь формулой 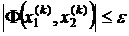 для каждого
для каждого  Го шага вычислений
Го шага вычислений 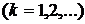 .
.
СИМПЛЕКС-МЕТОД.
ЗАДАНИЕ 3. Предположим, что в производстве двух видов продукции 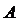 и
и 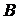 принимают участие три предприятия. При этом на изготовление единицы изделия
принимают участие три предприятия. При этом на изготовление единицы изделия 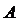 первое предприятие тратит
первое предприятие тратит 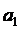 часов, второе предприятие -
часов, второе предприятие - 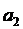 часов, третье предприятие -
часов, третье предприятие - 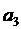 часов. На изготовление единицы продукции вида
часов. На изготовление единицы продукции вида 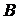 первое предприятие тратит
первое предприятие тратит  часов, второе предприятие -
часов, второе предприятие - 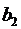 часов, третье предприятие -
часов, третье предприятие - 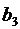 часов. На производство всех видов продукции первое предприятие может затратить не более, чем
часов. На производство всех видов продукции первое предприятие может затратить не более, чем 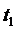 часов, второе предприятие - не более, чем
часов, второе предприятие - не более, чем 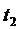 часов, третье предприятие - не более, чем
часов, третье предприятие - не более, чем 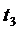 часов. От реализации единицы готовой продукции вида
часов. От реализации единицы готовой продукции вида 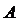 прибыль составляет
прибыль составляет  , а вида
, а вида 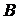 -
- 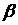 денежных единиц.
денежных единиц.
Составить математическую модель, определения максимальной прибыли от реализации всей продукции видов 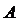 и
и 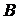 . Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки. Данные приведены в таблице данных.
. Решить задачу симплекс-методом. Дать геометрическую интерпретацию математической формулировки. Данные приведены в таблице данных.
Таблица данных.
|
№
Варианта
|
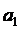
|
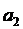
|
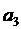
|

|
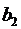
|
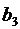
|
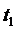
|
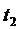
|
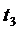
|

|
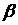
|
|
I
|
7
|
6
|
5
|
8
|
3
|
1
|
476
|
364
|
319
|
11
|
10
|
|
II
|
10
|
9
|
3
|
18
|
15
|
1
|
123
|
111
|
523
|
11
|
13
|
|
III
|
8
|
7
|
7
|
12
|
9
|
5
|
459
|
379
|
459
|
9
|
9
|
|
IV
|
8
|
7
|
7
|
10
|
5
|
2
|
612
|
492
|
562
|
11
|
9
|
|
V
|
10
|
9
|
5
|
6
|
3
|
1
|
735
|
765
|
455
|
8
|
4
|
|
VI
|
5
|
6
|
7
|
7
|
6
|
1
|
256
|
283
|
363
|
9
|
7
|
|
VII
|
3
|
9
|
10
|
5
|
3
|
2
|
414
|
723
|
788
|
12
|
16
|
|
VIII
|
7
|
7
|
8
|
5
|
2
|
1
|
347
|
300
|
357
|
11
|
7
|
|
IX
|
7
|
7
|
8
|
13
|
8
|
2
|
363
|
327
|
429
|
6
|
4
|
|
X
|
5
|
9
|
10
|
7
|
9
|
8
|
343
|
587
|
587
|
11
|
7
|
ТРАНСПОРТНАЯ ЗАДАЧА
ЗАДАНИЕ 4. Имеется три пункта поставки однородного груза 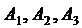 и пять пунктов
и пять пунктов  потребления этого груза. В пунктах поставки находится груз в количествах
потребления этого груза. В пунктах поставки находится груз в количествах 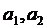 и
и 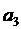 соответственно. В пункты потребления необходимо доставить груз в количествах соответственно
соответственно. В пункты потребления необходимо доставить груз в количествах соответственно 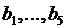 . Издержки на транспортировку единицы груза из пунктов поставки в соответствующие пункты потребления сведены в таблицу - матрицу издержек
. Издержки на транспортировку единицы груза из пунктов поставки в соответствующие пункты потребления сведены в таблицу - матрицу издержек 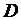 .
.
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты на перевозку были минимальными.
|
I.
|
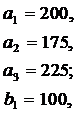
|
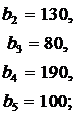
|
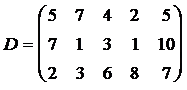 . .
|
|
II.
|
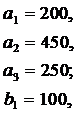
|
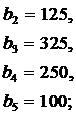
|
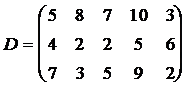 . .
|
|
III.
|
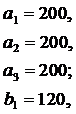
|
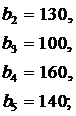
|
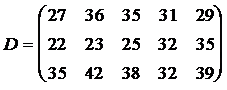 . .
|
|
IV.
|
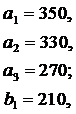
|
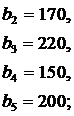
|
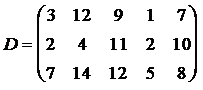 . .
|
|
V.
|

|
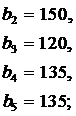
|
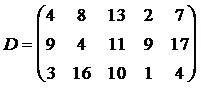 . .
|
|
VI.
|
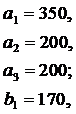
|

|
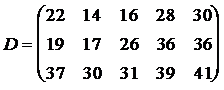 . .
|
|
VII.
|
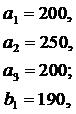
|
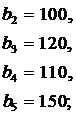
|
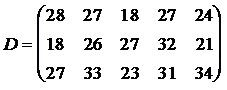 . .
|
|
VIII.
|

|
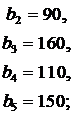
|
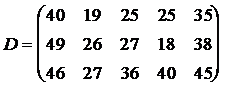 . .
|
|
IX.
|

|
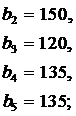
|
 . .
|
|
X.
|
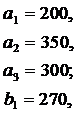
|
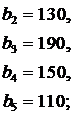
|
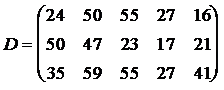 . .
|
ЦЕЛОЧИСЛЕННАЯ ЗАДАЧА
ЗАДАНИЕ 5. Найти экстремум целевой функции при заданной системе ограничений. Во всех задачах  Множество целых чисел.
Множество целых чисел.
|
I.
|
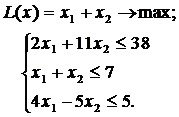
|
VI.
|
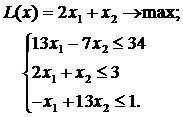
|
|
II.
|
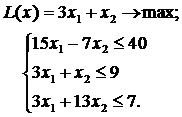
|
VII.
|
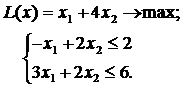
|
|
III.
|
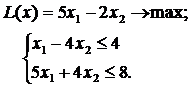
|
VIII.
|
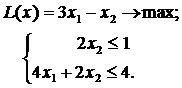
|
|
IV.
|

|
IX.
|
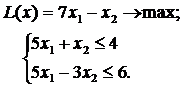
|
|
V.
|
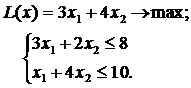
|
X.
|
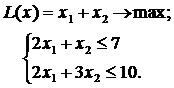
|
Эти задачи ввиду своей малой размерности позволяют выполнить вычисления вручную. Однако мы рекомендуем для расчетов дополнительно использовать вычислительную технику, например, вычислительные средства пакета прикладных программ “научного менеджмента” QSB.