Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

90. Распределения времени безотказной работы. Непрерывные распределения.

Некоторая система находится на испытаниях во внешних условиях, которые описываются случайным процессом, который имеет пиковые интенсивности (выбросы). Именно эти пиковые выбросы изменения внешних условий могут воздействовать на систему, которая может отказать только в момент указанного пикового воздействия.

1). Как и здесь, в большинстве случаев распределения, встречающиеся в практических приложениях, заметно несимметричны и не могут быть отнесены к нормальным.

2). Если поток выбросов является пуассоновским, то распределение отказов данной системы является экспоненциальным и в этих условиях предыстория системы не скажется на оставшейся длительности безотказной работы, то есть – все равно: система новая или уже была в работе.

3). Распределение отказов системы в этом случае описывается распределением Вейбулла

,

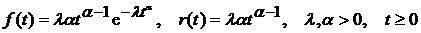Которое характеризуется убывающей интенсивностью отказов при 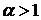(убывание неограниченное).

4). Гамма-распределение

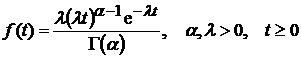
Является несимметричным распределением и не может быть использовано в качестве распределения отказов системы.

5). При 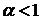интенсивность отказов гамма-распределения возрастает.

91. Монотонная функция интенсивности.

1). Если через 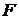обозначить распределение времени безотказной работы, то интенсивность отказов может быть определена выражением:

,

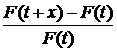Которое при фиксированных 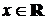вырождается в .

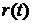2). Монотонную функцию интенсивности отказов имеет система с динамической нагрузкой.

3). И убывающая, и возрастающая функция интенсивности может быть определена не только для неотрицательных значений , но и для отрицательных.

4). Если распределение имеет возрастающую интенсивность отказов, то 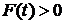для всех .

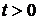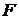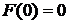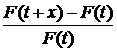5). Непрерывное распределение является монотонной функцией интенсивности тогда и только тогда, когда и является монотонной функцией от при 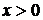, 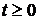таких, что .

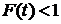92. Сохранение монотонности функции интенсивности.

1). Свойство убывания функции интенсивности не сохраняется при применении преобразований типа свертки.

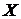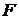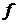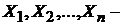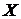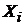2). Пусть есть случайная величина с возрастающей функцией интенсивности и плотностью . Если Независимые наблюдения случайной величины , то порядковые статистики образованные на , свойство монотонности не сохраняют.

3). Если 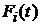есть убывающие функции интенсивности и 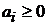для всех 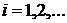, причем 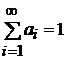, тогда 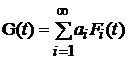– функция надежности системы есть убывающая функция интенсивности отказов.

4). Линейная комбинация возрастающих функций интенсивности обязательно сохраняет свойства монотонности.

5). Если 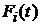есть возрастающие функции интенсивности и 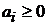для всех 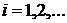, причем 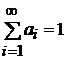, тогда 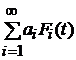– взвешенная сумма есть возрастающая функция интенсивности отказов.

ПП 2.9. Элементы теории восстановлений.

93. Элементы теории восстановления. Определения.

1). Процессом восстановления называют последовательность независимых, неотрицательных и одинаково распределенных случайных величин 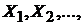которые все не равны нулю с вероятностью единица.

2). Одной из наиболее важных характеристик в теории восстановления является число восстановлений 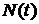в единицу времени.

3). Число восстановлений 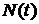на интервале времени 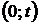Представляет собой максимальное значение величины , для которой 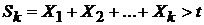при условии, что 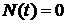, если .

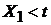4). Даже, если функция 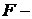Распределения случайной величины 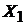является вырожденной, 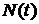имеет конечные моменты всех порядков.

5). Если 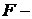возрастающая функция интенсивности отказов со средним значением 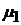, то для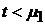

,

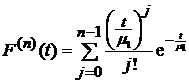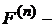
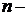Кратная свертка распределения .

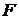94. Центральная предельная теорема для процесса восстановления.

1). Пусть существует конечная дисперсия DT = 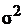интервала времени между событиями T. Тогда при 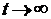имеет место сходимость по распределению

.

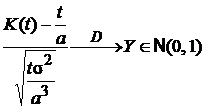2). Центральная предельная теорема позволяет при достаточно больших T аппроксимировать распределение случайной величины K(T) (сечения процесса в момент T) гипергеометрическим распределением.

3). Центральная предельная теорема позволяет при достаточно больших T аппроксимировать распределение случайной величины K(T) (сечения процесса в момент T) биномиальным распределением.

4). Центральная предельная теорема позволяет при достаточно больших T аппроксимировать распределение случайной величины K(T) (сечения процесса в момент T) равномерным распределением.

5). Центральная предельная теорема позволяет при достаточно больших T аппроксимировать распределение случайной величины K(T) (сечения процесса в момент T) пуассоновским распределением.

95. Функция восстановления.

1). Из определения функции восстановления следует, что 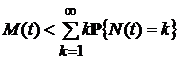, где 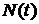– число восстановлений.

2). Если 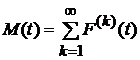, то .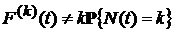

3). Функция восстановления 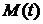определяется как среднее число восстановлений в интервале времени 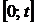, то есть .

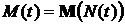4). Величина 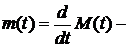плотность восстановления, однако: из 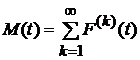не следует, что 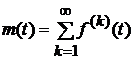, где .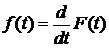

5). Если 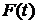имеет среднее 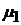. Тогда 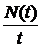сходится по вероятности к .

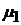96. Элементарная теорема восстановления и ее следствия.

1). Если распределение 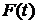имеет среднее значение 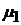, то .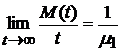

2). Если распределение 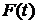имеет среднее значение 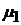, то .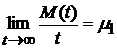

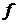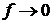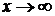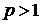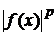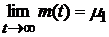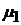3). Если такая плотность, что при , и если для некоторого функция интегрируема, то , где – среднее число восстановлений.

4). Если 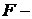убывающая функция интенсивности, то 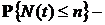Логарифмически выпуклая функция при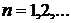

5). Функция 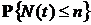не является выпуклой при 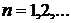, если 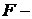возрастающая функция интенсивности.

97. Правила предупредительных замен.

1). Для бесконечного интервала времени критерием оптимизации является величина: 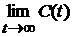, где 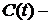Средние затраты в течение интервала времени .

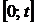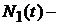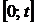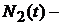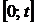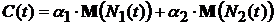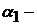2). Если Количество отказов в течение интервала времени , а Количество предупредительных замен за тот же промежуток времени. Средние затраты в течение интервала времени можно выразить в виде: , где Среднее время замены при отказе, 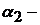Среднее время предупредительной замены.

3). Если распределение длительности безотказной работы является непрерывным, то оптимальное правило предупредительных замен заключается в выборе случайного периода замен.

4). Если известно лишь среднее значение 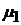распределения 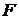(распределения времени безотказной работы) и неизвестен конкретный вид самого распределения, – правилом предупредительных замен на бесконечном отрезке времени является правило со случайным выбором.

5). Если известны лишь первые два момента 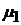и 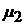, а конкретный вид распределения 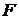не известен, причем: 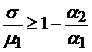(см. функцию затрат), то правило предупредительных замен состоит в заменах случайным образом.

98. Сложный процесс восстановления.

1). По аналогии с сложным пуассоновским процессом, сложный процесс восстановления отличается от простого (взвешенного) процесса восстановления тем, что веса образующих его событий являются случайными величинами Vi, которые, как и для сложного пуассоновского процесса, независимы в совокупности и имеют одинаковую функцию распределения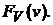

2). Сложный пуассоновский процесс представляет собой обобщение сложного процесса восстановления (при показательном распределении интервала времени между событиями).

3). Так же как и для сложного пуассоновского процесса, сложный процесс восстановления в общем случае можно представить в виде суперпозиции взвешенных простых процессов восстановления.

4). Так же как и для сложного пуассоновского процесса, сложный процесс восстановления в общем случае можно представить в виде линейной комбинации взвешенных простых процессов восстановления.

5). При достаточно малых интервалах наблюдения [0, T) (в сравнении с средним интервалом времени между событиями) применима предельная теорема, позволяющая аппроксимировать распределение с. в. 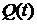показательным распределением, где 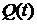– равна сумме весов Vi событий, происходящих на интервале времени [0, T).

99. Нормальный (гауссовский) случайный процесс.

1). Из этого определения следует, что любой конечномерный случайный вектор, образованный сечениями процесса X(T), имеет распределение Пуассона.

2). Из определения следует, что нормальный случайный процесс не может быть определен двумя известными моментными функциями: функцией математического ожидания (для стационарного процесса равной константе M) и корреляционной функцией.

3). Нормальным (гауссовским) случайным процессом называется случайный процесс, все конечномерные распределения которого имеют нормальное распределение.

4). Для стационарного нормального процесса функция математического ожидания не равна постоянной величине.

5). Нормальный случайный процесс не сохраняет тип распределения при линейных преобразованиях процесса.

100. Преобразования нормального случайного процесса.

1). Если, 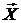– нормальный вектор, образованный N сечениями нормального процесса X(T), и Y(T) = B(T) X(T) + A(T) – его линейное преобразование. Тогда вектор 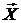преобразуется в нормальный вектор 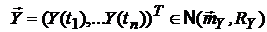, где 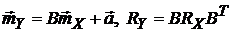, 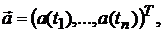B – матрица с элементами:

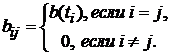
2). Если процесс X(T) дифференцируем в среднем квадратичном, то при DT®0 процесс Z(T) превращается процесс, представляющий собой производную процесса X(T), приобретая при этом распределение Пуассона.

3). Если процесс X(T) дифференцируем в среднем квадратичном, то при DT®0 процесс Z(T) превращается процесс, представляющий собой производную процесса X(T), приобретая при этом гипергеометрическое распределение.

4). Если процесс X(T) дифференцируем в среднем квадратичном, то при DT®0 процесс Z(T) превращается процесс, представляющий собой производную процесса X(T), приобретая при этом распределение арксинуса.

5). Если процесс X(T) дифференцируем в среднем квадратичном, то при DT®0 процесс Z(T) превращается процесс, представляющий собой производную процесса X(T), приобретая при этом распределение Мизеса.

• < Назад
• Вперёд >