Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Страница 5 из 9
42. Оптимальные стационарные стратегии. Оптимальные стратегии с дисконтом.
1). В цепях Маркова дисконтный множитель подбирается путем параметрической (одномерной) оптимизации по параметру 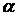 .
.
2). Дисконтный множитель в цепи Маркова является регуляризирующим параметром.
3). Для процессов, описываемых дискретными цепями Маркова, дисконтирующий множитель использовать невозможно, ввиду неслучайного его характера.
4). Дисконтирование, с точки зрения экономических приложений случайных процессов, дополняет схему поиска оптимальных стратегий в цепях Маркова. Полагая 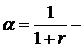 Дисконтный множитель (
Дисконтный множитель (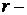 Процентная ставка), основное уравнение преобразуется к виду:
Процентная ставка), основное уравнение преобразуется к виду: 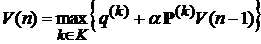 , где
, где 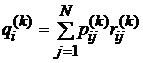 – по
– по 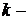 Му решающему правилу,
Му решающему правилу, 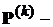 Матрица переходов,
Матрица переходов, 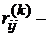 Элементы матрицы вознаграждений.
Элементы матрицы вознаграждений.
5). Оптимальную процентную ставку в дисконтирующем множителе для дискретной цепи можно определить как математическое ожидание стратегий на каждом шаге выбора.
43. Непрерывная цепь Маркова.
Задана матрица 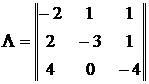 интенсивностей переходов непрерывной цепи Маркова. Укажите предельное распределение вероятностей:
интенсивностей переходов непрерывной цепи Маркова. Укажите предельное распределение вероятностей:
1). 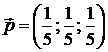 ; 2).
; 2).  ; 3).
; 3). 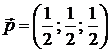 ;
;
4). 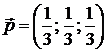 ; 5).
; 5). 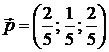 .
.
44. Возвратные состояния цепи Маркова.
1). Необходимым и достаточным условием возвратности I-го состояния однородной дискретной марковской цепи является равенство: 
2). Из необходимых и достаточных условий возвратности состояния следует, что ввиду недостаточности условия 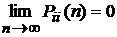 для сходимости ряда в
для сходимости ряда в 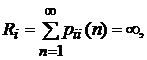 Нулевое состояние марковской цепи может быть только возвратным.
Нулевое состояние марковской цепи может быть только возвратным.
3). В связи с доказанной теоремой следует особо отметить, что ввиду недостаточности условия 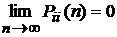 для сходимости ряда в
для сходимости ряда в 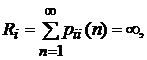 нулевое состояние марковской цепи может быть невозвратным. Очевидно, что ненулевое состояние цепи всегда возвратно.
нулевое состояние марковской цепи может быть невозвратным. Очевидно, что ненулевое состояние цепи всегда возвратно.
4). Однородная дискретная марковская цепь возвращается за конечное число шагов в исходное I-ое состояние с вероятностью 1 бесконечное число раз, если это состояние невозвратно, и лишь конечное число раз, если оно возвратно.
5). Только неоднородная дискретная марковская цепь возвращается за бесконечное число шагов в исходное I-ое состояние с вероятностью 1 бесконечное число раз, если это состояние невозвратно, и лишь конечное число раз, если оно возвратно.
45. Анализ свойств состояний дискретных марковских цепей.
1). Для неоднородной разложимой дискретной марковской цепи с ненулевыми состояниями справедливо равенство 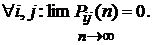
2). Все состояния конечной неоднородной неразложимой дискретной марковской цепи являются нулевыми (и, следовательно, возвратными).
3). Для неразложимой однородной дискретной марковской цепи справедливы следующие утверждения:
А) если одно из состояний такой цепи нулевое, то и все состояния нулевые;
Б) если одно из состояний возвратное, то и все возвратные;
В) если одно из состояний периодическое с периодом D, то и все состояния периодические с периодом D.
4). Дискретная марковская цепь называется эргодичной, если несуществует независимых от начального состояния ненулевых предельных (финальных) распределений вероятностей её состояний 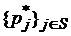 , удовлетворяющих условию:
, удовлетворяющих условию: 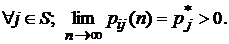
5). Стационарным распределением дискретной марковской цепи называется такое распределение вероятностей её состояний 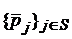 , которое изменяется только с течением времени (т. е. не зависит от N) и не зависит от начального состояния.
, которое изменяется только с течением времени (т. е. не зависит от N) и не зависит от начального состояния.
46. Эргодичность дискретной марковской цепи и существование её стационарного распределения.
1). Для того, чтобы конечная однородная дискретная марковская цепь была эргодичной, необходимо и достаточно, чтобы она была неразложимой и непериодической.
2). Для марковской цепи проявляющей свойство эргодичности, предельное распределение 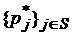 совпадает со стационарным распределением
совпадает со стационарным распределением 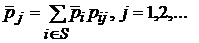 , которое неединственно.
, которое неединственно.
3). Для марковской цепи проявляющей свойство эргодичности, предельное распределение 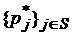 совпадает с нестационарным распределением
совпадает с нестационарным распределением 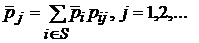 , которое неединственно.
, которое неединственно.
4). Вероятность 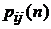 ограничена снизу и сверху сходящимися при
ограничена снизу и сверху сходящимися при 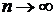 к общему пределу монотонными функциями, причем этот предел равен нулю, т. к. при достаточно больших
к общему пределу монотонными функциями, причем этот предел равен нулю, т. к. при достаточно больших 
5). Для марковских цепей с счетным множеством состояний, каждая такая марковская цепь может иметь только ненулевые состояния, причем они могут быть только невозвратными.
47. Эргодичность дискретной марковской цепи.
1). Класс всех дискретных однородных неразложимых непериодичных марковских цепей с счетным множеством состояний состоит из двух подклассов:
– подкласс A: цепи, все состояния которых нулевые; для них имеет место предельное соотношение 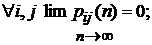
– подкласс B: цепи, все состояния которых ненулевые; для них существуют пределы 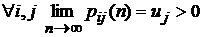 (здесь
(здесь 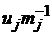 , Mj – по-прежнему среднее время возврата в J-ое состояние; для ненулевого состояния Mj<¥).
, Mj – по-прежнему среднее время возврата в J-ое состояние; для ненулевого состояния Mj<¥).
2). Если цепь принадлежит подклассу А (цепи, все состояния которых нулевые; для них имеет место предельное соотношение 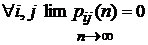 ), то она эргодична.
), то она эргодична.
3). Если цепь принадлежит к подклассу B (цепи, все состояния которых ненулевые; для них существуют пределы 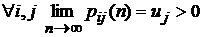 (здесь
(здесь 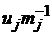 , Mj – по-прежнему среднее время возврата в J-ое состояние; для ненулевого состояния Mj<¥)), то она неэргодична.
, Mj – по-прежнему среднее время возврата в J-ое состояние; для ненулевого состояния Mj<¥)), то она неэргодична.
4). Для цепей Маркова класса В (цепи, все состояния которых ненулевые; для них существуют пределы 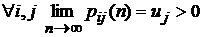 (здесь
(здесь 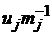 , Mj – по-прежнему среднее время возврата в J-ое состояние; для ненулевого состояния Mj<¥)), если стационарное распределение существует, то оно не единственно.
, Mj – по-прежнему среднее время возврата в J-ое состояние; для ненулевого состояния Mj<¥)), если стационарное распределение существует, то оно не единственно.
5). Эргодичность конкретной счетной марковской цепи можно проверять существованием для неё ненулевого положительного решения системы уравнений Колмогорова-Чепмена.
48. Марковские цепи с непрерывным аргументом.
1). Нельзя считать, что пуассоновский процесс при определенных значениях своих параметров представляет собой марковскую цепь с непрерывным аргументом.
2). Ступенчатый марковский процесс всегда имеет бесконечное (счетное) число состояний.
3). Ступенчатый процесс не является марковским.
4). Случайный процесс с непрерывным аргументом T и дискретным множеством состояния S, обладающий марковским свойством, называется марковской цепью с непрерывным аргументом.
5). Условия эргодичности процесса X(T), т. е. существования его предельного стационарного распределения невозможно получить, рассматривая ступенчатый процесс как предельный, возникающий из дискретной марковской цепи при неограниченном уменьшении шага дискретизации аргумента.
49. Непрерывные марковские процессы. Уравнения Колмогорова и Колмогорова-Фоккера-Планка.
1). При фиксированном значении любого сечения непрерывного Марковского процесса X=X(T) начальная скорость изменения условного математического ожидания процесса кусочно-постоянна и равна величине A(X,T), называемой коэффициентом сноса.
2). Для непрерывных Марковских процессов не существует ограниченной начальной скорости изменения условной дисперсии процесса B(X,T), именуемой коэффициентом диффузии.
3). Условие непрерывности процесса при выводе уравнения Колмогорова, может быть ослаблено, имея вид 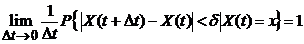 , где
, где 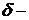 Бесконечно малое число.
Бесконечно малое число.
4). Второе уравнение Колмогорова (называемое также уравнением Колмогорова-Фоккера-Планка) имеет вид:
 ,
,
Где 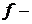 Функция плотности.
Функция плотности.
5). Условие непрерывности процесса при выводе уравнения Колмогорова, не может быть ослаблено.
ПП 2.5. Непрерывные цепи Маркова.
50. Вероятности состояний для произвольного момента времени, 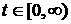 .
.
1). Граф состояний системы с заданными плотностями 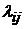 является неразмеченным графом системы.
является неразмеченным графом системы.
2). Недостаточно знать размеченный граф состояний системы для определения всех вероятностей  .
.
3). Если 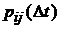 – вероятность того, что система, находящаяся в состоянии
– вероятность того, что система, находящаяся в состоянии 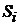 , за время
, за время 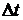 перейдет в состояние
перейдет в состояние 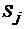 (
(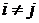 ), то величину
), то величину  – называют плотностью вероятности (интенсивностью) перехода из
– называют плотностью вероятности (интенсивностью) перехода из 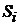 в
в 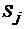 .
.
4). Известен размеченный граф состояний некоторой системы:
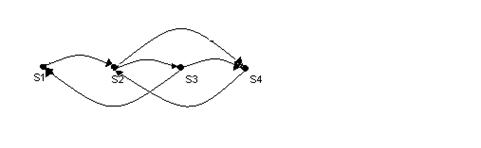
Тогда прямая система дифференциальных уравнений Колмогорова имеет вид:
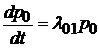 ,
,
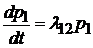 ,
,
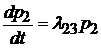 ,
,
 .
.
5). Матрица системы уравнений Колмогорова является симметричной положительно определенной матрицей.
51. Предельные вероятности состояний, 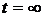 .
.
1). Если  – вероятность пребывания системы в состоянии
– вероятность пребывания системы в состоянии 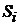 в момент времени
в момент времени  . Пределы
. Пределы 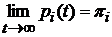 , если они существуют, называются предельными (финальными) вероятностями состояний системы.
, если они существуют, называются предельными (финальными) вероятностями состояний системы.
2). Для того, что бы предельные вероятности состояний системы существовали, пространство состояний системы должно быть счетным: 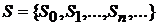 .
.
3). Если пространство состояний 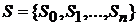 системы конечно и из каждого состояния
системы конечно и из каждого состояния 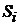 за конечное число шагов можно перейти в любое другое состояние
за конечное число шагов можно перейти в любое другое состояние 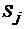 (все состояния марковской цепи – сообщающиеся), то предельных вероятностей
(все состояния марковской цепи – сообщающиеся), то предельных вероятностей 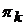 состояний система не имеет.
состояний система не имеет.
4). Для вычисления предельных вероятностей состояний системы необходимо правые части системы уравнений Колмогорова считать постоянными.
5). Если система имеет предельные вероятности состояний 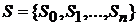 , то из каждого состояния
, то из каждого состояния 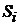 можно перейти в любое другое состояние только за бесконечное число шагов.
можно перейти в любое другое состояние только за бесконечное число шагов.
52. Процесс гибели и размножения. Уравнения Колмогорова для вероятностей состояний, 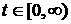 .
.
1). Процесс гибели и размножения для дискретной цепи Маркова определяется матрицей плотностей вероятностей перехода 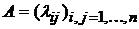 с элементами
с элементами
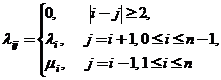 ,
, 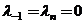 ,
,
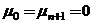 .
.
Параметры 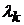 характеризуют рождаемость, а параметры
характеризуют рождаемость, а параметры 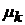 – смертность. Предельное распределение вероятностей
– смертность. Предельное распределение вероятностей 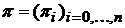 состояний цепи Маркова
состояний цепи Маркова 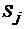 ,
, 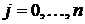 , в терминах параметров
, в терминах параметров 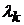 и
и 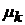 определяется основными соотношениями
определяется основными соотношениями
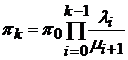 ,
, 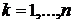 ,
, 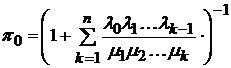 .
.
2). Размеченный граф состояний системы, соответствующий процессу гибели и размножения не может иметь следующий вид:

3). Общий метод получения одномерного распределения обобщенного процесса гибели и размножения 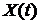 , т. е. вероятностей
, т. е. вероятностей 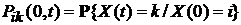 , не предполагает использование уравнений Колмогорова-Чепмена.
, не предполагает использование уравнений Колмогорова-Чепмена.
4). Среди характеристических чисел матрицы системы уравнений Колмогорова для процессов гибели и размножения есть кратные.
5). Характеристические числа матрицы системы уравнений Колмогорова для процессов гибели и размножения в спектр матрицы входят парами с комплексно сопряженными им числами.