Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Страница 4 из 9
27. Дискретная цепь Маркова. Матрицы перехода.
Задана матрица  вероятностей перехода дискретной цепи Маркова из I-го состояния в J-ое за один шаг (I, J=1, 2). Распределение вероятностей по состояниям в начальный момент T=0 определяется вектором
вероятностей перехода дискретной цепи Маркова из I-го состояния в J-ое за один шаг (I, J=1, 2). Распределение вероятностей по состояниям в начальный момент T=0 определяется вектором  =(0,1; 0,9). Укажите матрицу Р2 перехода цепи из состояния I в состояние J за два шага:
=(0,1; 0,9). Укажите матрицу Р2 перехода цепи из состояния I в состояние J за два шага:
1).  ; 2).
; 2).  ; 3).
; 3). 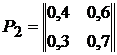 ;
;
4). 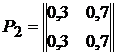 ; 5).
; 5).  .
.
28. Дискретная цепь Маркова. Неустановившиеся состояния.
Неустатовившимся состоянием марковской цепи называется состояние с нулевой стационарной вероятностью. Для цепи Маркова, которая имеет матрицу вероятностей перехода
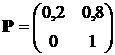
Укажите состояние, которое можно оценить как неустановившееся:
1). Второе;
2). Третье;
3). Четвертое;
4). Первое;
5). Пятое.
29. Дискретная цепь Маркова. Поглощающие состояния.
Рассмотрим цепь Маркова с матрицей вероятностей перехода:
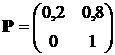 .
.
Для системы укажите состояние, которое является поглощающим:
1). Первое;
2). Третье;
3). Второе;
4). Четвертое;
5). Пятое.
30. Дискретная цепь Маркова. Периодическое (циклическое) состояние.
По матрице вероятностей перехода:
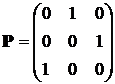
Порождающей цепь Маркова, можно судить о периодическом, или циклическом, поведении. Начиная с состояния 1, система попадает в это же состояние в следующие периоды:
1). 2, 4, 6, …;
2). 2, 3, 4, …;
3). 3, 6, 9, …;
4). 3, 5, 7, …;
5). 3, 4, 5, …
31. Дискретная цепь Маркова. Периодические множества.
Если система имеет такое множество состояний, что, однажды попав в него, она может осуществлять переходы только внутри множества и никогда не покинет его. Такое множество называют периодическим. Укажите периодическое множество для системы с матрицей переходов:
 .
.
1). Единственное состояние 1;
2). Только состояние 2;
3). Состояния 1, 2 и 3;
4). Состояния 1 и 2;
5). Только состояние 3.
32. Дискретная цепь Маркова. Распределение вероятностей по состояниям.
Задана матрица  вероятностей перехода дискретной цепи Маркова из I-го состояния в J-ое за один шаг (I, J=1, 2). Распределение вероятностей по состояниям в начальный момент T=0 определяется вектором
вероятностей перехода дискретной цепи Маркова из I-го состояния в J-ое за один шаг (I, J=1, 2). Распределение вероятностей по состояниям в начальный момент T=0 определяется вектором  =(0,1; 0,9). Укажите распределение вероятностей по состояниям в момент T=2:
=(0,1; 0,9). Укажите распределение вероятностей по состояниям в момент T=2:
1). 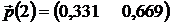 ; 2).
; 2). 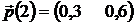 ; 3).
; 3). 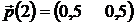 ;
;
4).  ; 5).
; 5). 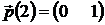 .
.
33. Дискретная цепь Маркова. Стационарное распределение.
Задана матрица  вероятностей перехода дискретной цепи Маркова из I-го состояния в J-ое за один шаг (I, J=1, 2). Распределение вероятностей по состояниям в начальный момент T=0 определяется вектором
вероятностей перехода дискретной цепи Маркова из I-го состояния в J-ое за один шаг (I, J=1, 2). Распределение вероятностей по состояниям в начальный момент T=0 определяется вектором  =(0,1; 0,9). Укажите стационарное распределение:
=(0,1; 0,9). Укажите стационарное распределение:
1).  ; 2).
; 2). 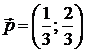 ; 3).
; 3).  ; 4).
; 4).  ; 5).
; 5). 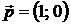 .
.
34. Дискретные цепи Маркова. Свойство эргодичности.
1). Система является эргодической, если переход из произвольного состояния в любое другое состояние возможен за конечное число шагов.
2). Система обладает свойством эргодичности, если ее полное множество состояний не является периодическим.
3). Если система обладает свойством эргодичности, то она имеет несколько (более одного) периодических множеств состояний.
4). Если система не обладает свойством эргодичности, то для нее существуют обязательно стационарные вероятности.
5). Наличие периодических множеств состояний не связано с существованием стационарных вероятностей состояний этой же системы.
35. Дискретные цепи Маркова. Приложения.
Для системы с переходной матрицей:
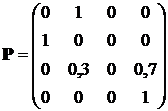 ,
,
Состояния:
1). 1 – поглощающее, 4 – переходное, 2 и 3 – периодическое множество;
2). 1 – переходное, 2 – поглощающее, 3 и 4 – периодическое множество;
3). 1 и 4 – периодическое множество, 2 – поглощающее, 3 – переходное;
4). 1 и 2 – периодическое множество, 3 – переходное, 4 – поглощающее;
5). 1 и 3 – периодическое множество, 4 – поглощающее.
36. Существование стационарных вероятностей для дискретных цепей Маркова.
1). Марковская цепь регулярна, если существует некоторое целое положительное число 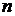 , такое, что любой элемент матрицы
, такое, что любой элемент матрицы 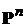 , исключая элементы, относящиеся к переходным состояниям, больше нуля.
, исключая элементы, относящиеся к переходным состояниям, больше нуля.
2). Марковская цепь регулярна, если существует некоторое целое положительное число 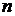 , такое, что любой элемент матрицы
, такое, что любой элемент матрицы 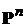 , включая элементы, относящиеся к переходным состояниям, строго больше нуля.
, включая элементы, относящиеся к переходным состояниям, строго больше нуля.
3). Для существования стационарных вероятностей, регулярность матрицы переходов должна быть исключена.
4). Если цепь регулярна, то не существует предельной матрицы  .
.
5). При проверке системы на регулярность рассматриваются все ее переходные состояния.
37. Стационарные вероятности дискретных Марковских цепей.
Марковская цепь с матрицей переходов

– регулярна. При этом 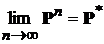 , где
, где 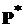 – матрица вида:
– матрица вида:
1).  ; 2).
; 2).  ; 3).
; 3).  ;
;
4).  ; 5).
; 5). 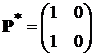 .
.
38. Марковские цепи с вознаграждением.
1). Если матрица переходов системы не является регулярной, то возможно найти стационарное ожидаемое вознаграждение, в силу существования стационарных вероятностей.
2). Стационарное ожидаемое вознаграждение представляет собой взвешенную сумму: 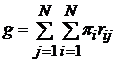 , где
, где  Вектор стационарных вероятностей.
Вектор стационарных вероятностей.
3). Стационарное ожидаемое вознаграждение может быть определено только для систем с периодическим множеством.
4). Для регулярных систем матрица вознаграждений всегда вырождена и стационарные вознаграждения на бесконечном промежутке времени равны нулю.
5). Суммарное ожидаемое вознаграждение за 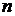 периодов, начинающихся с состояния
периодов, начинающихся с состояния  , может быть записано как
, может быть записано как
 ,
,
Где 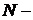 Число состояний системы,
Число состояний системы, 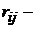 Элементы матрицы вознаграждений
Элементы матрицы вознаграждений 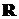 размерности
размерности  ,
, 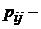 Вероятность перехода из состояния
Вероятность перехода из состояния  в состояние
в состояние  .
.
39. Стационарное ожидаемое вознаграждение.
Пусть система имеет следующую матрицу переходов:
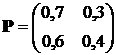 , а
, а  – матрица вознаграждений. Тогда стационарное ожидаемое вознаграждение
– матрица вознаграждений. Тогда стационарное ожидаемое вознаграждение  равно:
равно:
1). 1; 2). 2; 3). 1,2; 4). Меньше 1; 5). Больше 2.
40. Оптимальные стратегии в марковских цепях.
1). Общий подход к решению проблемы определения оптимальной стратегии состоит в рассмотрении 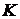 различных правил, определяющих соответствующие решения.
различных правил, определяющих соответствующие решения.
2). Максимальное ожидаемое вознаграждение за 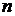 периодов определяется уравнениями:
периодов определяется уравнениями: 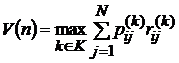 ,
, 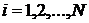 .
.
3). Множество решений уравнений 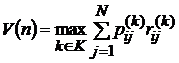 ,
, 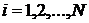 образует оптимальную стратегию.
образует оптимальную стратегию.
4). Оптимальная стратегия в марковских цепях – это вектор, компоненты которого определяются одновременно для каждого возможного состояния системы.
5). Оптимальная стратегия в марковских цепях – это вектор со случайными компонентами.
41. Определение оптимальной стратегии в дискретной цепи Маркова.
Имеется марковская цепь с двумя решающими правилами. Правилу 1 (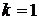 ) соответствует матрица переходов
) соответствует матрица переходов
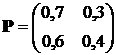 с вознаграждением
с вознаграждением  .
.
Правилу 2 (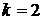 ) соответствует матрица переходов
) соответствует матрица переходов
 с вознаграждением
с вознаграждением  .
.
Определите оптимальную стратегию, дающую максимальное ожидаемое вознаграждение:
1).  ; 2).
; 2).  ; 3).
; 3). 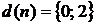 ;
;
4). 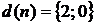 ; 5).
; 5).  .
.