Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

17. Интегрирование случайных процессов.

1). Интегралом Римана от случайного процесса второго порядка 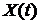в среднем квадратичном (стохастическим интегралом Римана в среднем квадратичном) с функцией 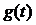на интервале называется предел в с. к. 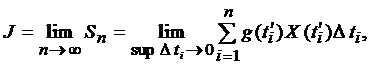если он существует и одинаков при любом разбиении на непересекающиеся полуинтервалы. Примем обозначение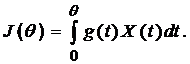

2). Необходимым и достаточным условием интегрируемости случайного процесса второго порядка 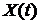с ограниченным моментом второго порядка (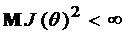) является существование конечного интеграла

<¥.

3). Условие существование конечного интеграла <¥. – существования интеграла 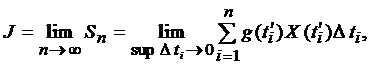в общем случае не может быть заменено условием существования ограниченных интегралов: и

4). Для непрерывных случайных процессов в общем случае .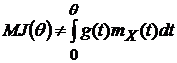

5). При интегрировании случайного процесса X(T) получается случайный процесс 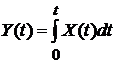того же порядка. Однако оба являются некоррелированными и .

18. Переходные функции случайного процесса. Марковское свойство.

1). Переходной функцией распределения процесса 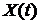называется функция , .

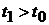2). Переходные функции случайных процессов представляют собой условные функции распределения процесса и содержат информацию о поведении случайного процесса в момент времени .

3). Случайный процесс 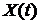называется однородным, если его переходная функция распределения зависит только от от отдельных значени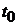й и .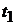

4). Марковское свойство случайного процесса 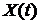имеет вид: .

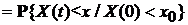5). Случайный процесс c дискретным пространством состояний 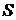и дискретным (непрерывным) временем заведомо не может обладать марковским свойством.

ПП 2.3. Стационарность и эргодичность случайных процессов.

19. Стационарность случайных процессов.

1). Моментные функции строго стационарных процессов второго порядка, как и в общем случае, не являются постоянными величинами.

2). Случайный процесс X(T) называется строго стационарным (или стационарным в узком смысле), если все его конечномерные распределения не изменяются при эквидистантном изменении аргументов T1, … Tn, т. е. если

3). Класс случайных процессов, рассматриваемых как стационарные, невозможно расширить, если ограничить условия стационарности равенствами:

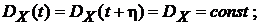
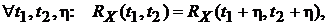
Или, принимая h= – T1,

4). Случайный процесс X(T) называется стационарным (или стационарным в широком смысле), если его моментные функции постоянные величины.

5). Строго стационарные процессы не всегда являются стационарными в широком смысле.

20. Свойства корреляционной функции стационарного процесса.

Свойства корреляционной функции вещественного случайного процесса для стационарного процесса очевидным образом принимают вид:

1). ;

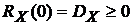2). ;

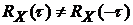3). ;

4). .

5).Непрерывность при не связана с непрерывностью для всех .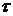

21. Эргодичность случайных процессов.

1). Из эргодичности случайного процесса в среднем квадратичном не следует его эргодичность и по вероятности.

2). Необходимым и достаточным условием эргодичности в среднем квадратичном по математическому ожиданию стационарного случайного процесса второго порядка является существование предела

3). Эргодичность X(T) по дисперсии означает эргодичность случайного процесса по математическому ожиданию.

4). Стационарный случайный процесс X(T) эргодичен в среднем квадратичном по математическому ожиданию, если его среднее значение по аргументу áХñQ Сходится при 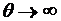в среднем квадратичном к значению математического ожидания .

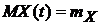5). Эргодичность X(T) по корреляционной функции есть эргодичность по математическому ожиданию случайного процесса от двух аргументов (случайного поля) .

ПП 2.4. Марковский случайный процесс. Цепи Маркова.

22. Марковский случайный процесс.

1). Марковский процесс c дискретным пространством состояний 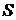и только дискретным временем называется марковской цепью.

2). Марковский процесс с непрерывным временем не может порождать Марковскую цепь.

3). Случайный процесс, обладающий марковским свойством:

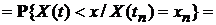
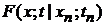
Называется марковским случайным процессом.

4). В силу марковского свойства, если известно состояние процесса в момент времени , то этой информации не достаточно чтобы предсказывать поведение процесса в последующие моменты времени.

5). Для некоторых марковских процессов имеет место свойство:

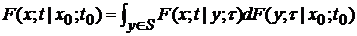, – уравнение Колмогорова-Чепмена.

23. Марковские цепи.

1). Если стационарное распределение цепи Маркова 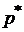, то существует и предельное ее (цепи Маркова) состояние , такое, что: .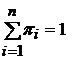

2). Для предельных состояний цепи Маркова: .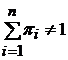

3). Пусть 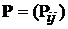– одношаговая переходная вероятность марковской цепи с дискретным временем, 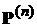– 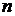-шаговая переходная вероятность. Матрица 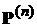– не является стохастической.

4). Марковская цепь – это марковский процесс с дискретным множеством состояний.

5). Вектор вероятностей 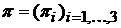для матрицы переходных вероятностей

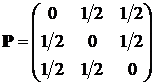
Цепи Маркова имеет вид: .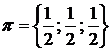

24. Классификация состояний марковской цепи.

1). Если состояние не относится к несущественным, то это не значит, что оно является существенным. Такое состояние обладает тем свойством, что при выходе из него в любое другое состояние система возвращается в него с ненулевой вероятностью.

2). Назовем I-ое состояние марковской цепи несущественным, если и для 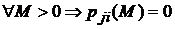. Другими словами для каждого несущественного состояния марковской цепи существует хотя бы одно состояние, в которое цепь переходит с положительной вероятностью и из которого ни за какое число шагов она не может вернуться в прежнее состояние.

3). Будем, далее, именовать I-ое состояние марковской цепи невозвратным, если, находясь в этом состоянии, цепь с вероятностью единица невозвращается в него за конечное число шагов.

4). Обозначим An событие, состоящее в том, что цепь, находясь в I-ом состоянии, впервые вернется в него ровно за N шагов. Вероятность этого события равна Тогда вероятность возвращения в I-ое состояние за конечное число шагов равна

5). Если то I-ое состояние является возвратным; в противном случае (если ) это состояние относится к невозвратным, где , An событие, состоящее в том, что цепь, находясь в I-ом состоянии, впервые вернется в него ровно за N шагов. Вероятность этого события равна

25. Некоторые свойства Марковских цепей.

1). Некоторые I-ое и J-ое несущественные состояния марковской цепи являются сообщающимися, если .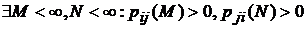

2). Свойство состояний быть сообщающимися разбивает все множество состояний цепи S на счетное число классов эквивалентности.

3). Марковская цепь, все состояния которой образуют один класс сообщающихся состояний S, является разложимой (или приводимой).

4). Пусть в начальный момент марковская цепь находилась в I-ом состоянии и – вероятность того, что на N-ом шаге она вновь окажется в этом состоянии (не обязательно в первый раз). Если 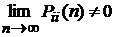, то I-ое состояние называется ненулевым.

5). Марковская цепь, все состояния которой образуют один класс сообщающихся состояний S, называется неразложимой (или неприводимой). В общем случае марковская цепь может состоять из конечного или счетного множества классов сообщающихся состояний 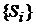и класса несущественных состояний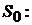

26. Матрица переходных вероятностей.

1). Пусть 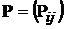– матрица переходных вероятностей конечной цепи Маркова. Тогда 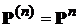. Если 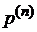– вектор состояний системы через 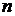шагов, то .

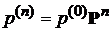2). Предположим, что после очень большого числа периодов вектор состояний 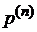в период 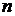отличается от вектора состояний 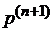в период 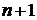на бесконечно малую величину и независим от начального вектора состояний 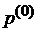, то такой вектор 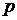называют стационарным вектором марковской цепи.

3). Неустановившимся состоянием марковской цепи называется состояние с ненулевой стационарной вероятностью.

4). Установившимся состоянием марковской цепи называется состояние с нулевой стационарной вероятностью.

5). Если марковская цепь имеет одно или более переходных состояний, из этого следует существование поглощающего состояния этой же марковской цепи.

• < Назад
• Вперёд >