Лекция ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ

10. Ковариационная функция случайного процесса.

1). Ковариационная функция равна математическому ожиданию произведения двух нецентрированных сечений случайного процесса и имеет вид:

Для дискретного случая.

2). Непрерывного аналога ковариационная функция не имеет.

3). Ковариационная функция, представляет собой второй центральный момент двух сечений процесса X(T).

4). Моментные функции существуют при всех значениях аргументов, что обеспечивается абсолютной сходимостью выражающих их рядов и интегралов.

5). По определению , однако .

11. Свойства корреляционной функции случайного процесса.

1). Из свойства симметричности конечномерных распределений с. п. вовсе не следует симметричность к. ф.: .

2). Ввиду неотрицательности дисперсии вещественной случайной величины имеет место соотношение .

3). При любом наборе совокупность значений корреляционной функции образуют корреляционную матрицу , которая в силу отрицательной определенности корреляционной функции так же отрицательно определена.

4). В связи со свойством отрицательной определенности корреляционной функции заметим, что если существует отличный от нуля вектор , для которого при некотором имеет место:

То сечения случайного процесса линейно независимы.

5). По определению , однако .

12. Простейшие преобразования случайных процессов.

1). Функция описывает корреляционную связь между значениями случайных процессов X(T) и Y(T) в различные моменты времени.

По определению, из = Þ = .

2). Рассмотрим преобразование вида Y(T) = A(T)X(T) + B(T). Здесь X(T) – «входной» случайный процесс, обладающий математическим ожиданием MX(T) и корреляционной функцией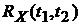, Y(T) – «выходной» (преобразованный) случайный процесс, A(T), B(T) – ограниченные неслучайные функции. Из свойств математического ожидания следует:

.

3). Рассмотрим преобразование вида Y(T) = A(T)X(T) + B(T). Здесь X(T) – «входной» случайный процесс, обладающий математическим ожиданием MX(T) и корреляционной функцией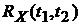, Y(T) – «выходной» (преобразованный) случайный процесс, A(T), B(T) – ограниченные неслучайные функции. Для корреляционной функции имеем соотношение: .

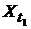4). Взаимной корреляционной функцией случайных процессов X(T) и Y(T), определенным на общем вероятностном пространстве, называется неслучайная функция RXY, которая для каждой пары значений аргументов T1 и T2 равна корреляционному моменту сечений И этих процессов, т. е.

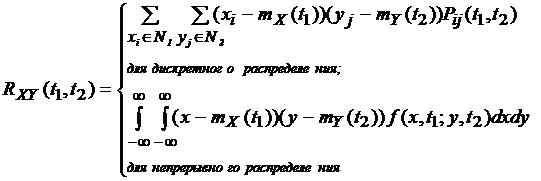
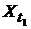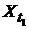(здесь N1 и N2 – множество значений сечений и , –функция и плотность совместного распределения сечений и ).

5). Рассмотрим преобразование вида Y(T) = A(T)X(T) + B(T). Здесь X(T) – «входной» случайный процесс, обладающий математическим ожиданием MX(T) и корреляционной функцией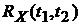, Y(T) – «выходной» (преобразованный) случайный процесс, A(T), B(T) – ограниченные неслучайные функции. Для дисперсии имеем соотношение: .

13. Простейшие преобразования случайных процессов.

Преобразование вида . Здесь – совокупность случайных процессов, определенных на общем вероятностном пространстве и обладающих математическими ожиданиями , корреляционными функциями и взаимными корреляционными функциями 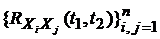, – неслучайные ограниченные функции.

1). Функция математического ожидания:

.

2). Корреляционная функция: .

3). Функция дисперсии: .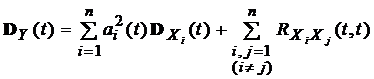

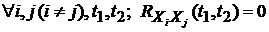4). Если случайные процессы взаимно некоррелированы, т. е. , то .

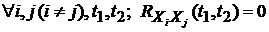5). Если случайные процессы взаимно некоррелированы, т. е. , то .

ПП 2.2. Дифференцирование и интегрирование случайных процессов

14. Определения сходимости и непрерывности.

Рассматривается сходимость последовательности случайных величин к случайной (в общем случае) величине Х В среднем квадратичном («в с. к.»), т. е. такая, что . Для такого типа сходимости используются обозначения: или .

1). Случайный процесс второго порядка непрерывен при значении аргумента T, если выполнено условие

2). Случайный процесс второго порядка непрерывен в среднем квадратичном, если Выполняется для всех T Î T.

3). Пусть , , X и Y – случайные величины, заданные на одном вероятностном пространстве, и Тогда .

4). Для случайных процессов, непрерывность в среднем квадратичном вовсе не означает, что среднее значение квадрата разности двух сечений случайного процесса стремится к нулю по мере сближения этих сечений.

5). Непрерывность случайного процесса в среднем квадратичном, по сути, означает, что среднее значение квадрата разности двух сечений случайного процесса стремится к нулю по мере их удаления во времени.

15. Производная с. п. в среднем квадратичном.

1). Случайный процесс второго порядка Х(T) является дифференцируемым в среднем квадратичном в точке T, если в этой точке он непрерывен.

2). Существование производной является необходимым, но не достаточным условием существования в точке T производной в среднем квадратичном c ограниченным моментом второго порядка случайного процесса второго порядка Х(T).

3). Достаточным условием существования в точке T производной в среднем квадратичном c ограниченным моментом второго порядка случайного процесса второго порядка Х(T) является существование у случайного процесса ограниченной производных математического ожидания .

4). Производной случайного процесса второго порядка Х(T) в среднем квадратичном в точке T называется предел .

5). Существование производной и ограниченных производных математического ожидания и корреляционной функции не является равносильным условием существования производной случайного процесса.

16. Производная с. п. в среднем квадратичном.

1). Для математического ожидания производной случайного процесса имеем:

2). Для корреляционной функции случайного процесса имеем:

.

3). Для дисперсии:

.

4). Выражение для взаимной корреляционной функции случайного процесса 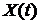и его производной : .

5). Если необходимые и достаточные условия существования производной случайного процесса Х(T) выполнены для , то в результате дифференцирования в среднем квадратичном случайного процесса второго порядка Х(T) возникает процесс X¢(T) также второго порядка.

• < Назад
• Вперёд >