Лекция методы исследования операций

44. Методы решения игр.

Основными методами решения матричных игр двух игроков являются (укажите тот, который к игровым моделям не относится):

1). Графический метод.

2). Метод выделения подматриц.

3). Метод последовательных приближений.

4). Решение игры путем сведения ее к задаче линейного программирования.

5). Метод сопряженных градиентов.

45. Коалиционные игры.

1). После ходов (один ход на одного игрока) игрок 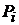получает платеж 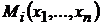. Если игра имеет нулевую сумму, то

.

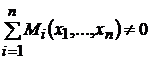2). Если все игроки группируются в две коалиции, это вовсе не значит, что игру можно свести к игре двух игроков с нулевой суммой.

3). Если все игроки вступят в одну коалицию, то цена игры (характеристическая функция) .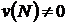

4). При конфликтной ситуации, в которой участвуют более двух игроков, возникает проблема образования коалиций. В этом случае смешанные стратегии и цена игры являются функциями различных вариантов коалиций. Такие игры называются коалиционными.

5). Характеристическая функция четна .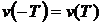

46. Свойства характеристических функций.

1). Характеристическая функция коалиционной игры имеет вид:

,

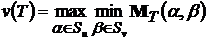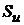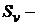Где и Множества смешанных стратегий коалиций.

2). Если и 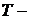Непересекающиеся подмножества множества , то .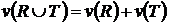

3). Если 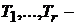Непересекающиеся подмножества множества , сумма которых есть , то .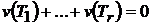

4). Если две игры отличаются платежными и характеристическими функциями, то они стратегически не эквивалентны.

5). Характеристическая функция 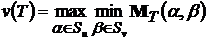определена не для всяких подмножеств .

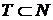47. Стратегические свойства в коалиционных играх.

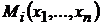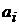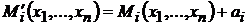
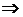
1). Если к платежной функции прибавить некоторую константу , которая обладает тем свойством, что для 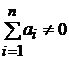, – вновь полученная игра не будет стратегически эквивалентной исходной игре.

2). Если изменить масштаб платежей, заданных функцией 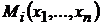, с помощью умножения на какой-либо скаляр 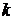, то полученная игра с функцией 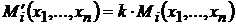будет характеризоваться теми же стратегическими свойствами, что и исходная.

3). Значение 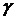– модуль приведенной формы игры может принимать значения 0 и 1.

4). Всякая характеристическая функция стратегически эквивалентна некоторому конечному множеству характеристических функций в приведенной форме.

5). Игры в приведенной форме с модулем –1 не имеют тенденции к образованию коалиций и называются несущественными (по существу некоалиционными).

48. Модели непрерывных игр.

1). Платежная функция непрерывной игры седловых точек не имеет и, следовательно, игра решается в смешанных стратегиях.

2). Если точка 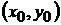является седловой точкой платежной функции, то имеет место соотношение: .

3). Для определения среднего платежа в непрерывной игре необходимо задание вероятностного пространства событий, связанных с выбором стратегий игроков.

4). Непрерывная игра задается платежной функцией 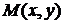, где 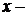Стратегия первого игрока, 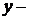Стратегия второго игрока.

5). В общем случае непрерывных или непрерывно-дискретных игр всегда существуют функции цен в смысле максиминных и минимаксных выражений.

49. Свойства оптимальных стратегий.

1). Плотности распределения вероятностей имеют вид:

Здесь , .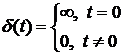

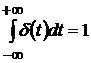2). В непрерывных играх у каждого игрока имеются, по крайней мере, по одной чистой стратегии.

3). Платежная функция в непрерывных играх не отвечает условиям выпуклости.

4). Если 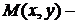Платежная функция непрерывной игры, является вогнутой, то у одного из игроков имеется единственная оптимальная стратегия, а у второго имеется оптимальная чистая стратегия, такая, что:

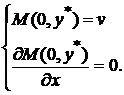
5). В отличие от дискретных игр, в непрерывных играх существуют методы решения в том смысле, что существует конечный процесс определения оптимальных стратегий.

ПП 6.5. Игры с природой.

50. Критерий среднего выигрыша.

1). Эффективность систем оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по состояниям, принадлежащих некоторому множеству :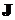

.

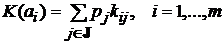2). Критерий среднего выигрыша предполагает задание вероятностей состояний обстановки .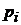

3). Оптимальной системе соответствует эффективность:

.

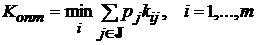4). Для применения критерия среднего выигрыша необходим перевод операции из неопределенной в вероятностную по некоторому определенному правилу.

5). Для применения критерия среднего выигрыша необходим перевод операции из неопределенной в детерминированную.

51. Критерий Лапласа. Критерий осторожного наблюдателя (Вальда).

1). Исходя из предположения равновероятности состояний обстановки

.

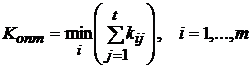2). Критерий Лапласа не является частным случаем критерия среднего выигрыша.

3). В основе критерия Лапласа лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными.

4). Критерий Вальда основывается на том, что, если состояние обстановки неизвестно, то необходимо ориентироваться на максимальное значение эффективности каждой системы.

5). Согласно критерию Вальда:

.

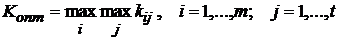52. Критерий писсемизма-оптимизма (Гурвица).

1). Условие оптимальности критерия Гурвица записывается в виде:

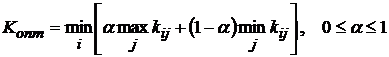
2). При 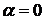критерий Гурвица сводится к критерию максимакса.

3). При 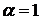критерий Гурвица сводится к критерию максимина.

4). Критерий Гурвица – это критерий обобщенного максимина: при оценке и выборе систем неразумно проявлять как осторожность, так и азарт, а следует учитывать самое высокое и самое низкое значения эффективности, занимать промежуточную позицию.

5). Наиболее часто употребительным значением коэффициента оптимизма является .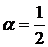

53. Критерий минимального риска (Сэвиджа).

1). Для использования критерия Сэвиджа нет необходимости в преобразованиях матрицы эффективности.

2). Критерий Сэвиджа нельзя отнести к осторожным критериям.

3). Критерий оптимальности имеет вид: 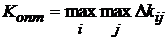, где 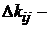Элементы матрицы рисков.

4). Критерий Сэвиджа не всегда дает оптимальное решение задачи.

5). Критерий Сэвиджа минимизирует потери эффективности при наихудших условиях.

ПП 6.6. Потоковые модели.

54. Задачи, решаемые методами теории потоков.

1). В отличие от евклидовых, прямоугольных, криволинейных и других пространств, в графовых моделях используются концепции топологических геометрий и пространств.

2). Под транспортной сетью понимается плоский граф, в котором могут присутствовать петли, есть начальная вершина (исток) и конечная вершина (сток).

3). Истоком называют вершину транспортной сети, если единственная дуга графа в нее входит, а все остальные дуги выходят.

4). Стоком называют вершину транспортной сети, если единственная дуга из нее исходит, а все остальные дуги входят.

5). Транспортная сеть может иметь несколько истоков и несколько стоков.

55. Основные понятия и определения теории потоков.

1). Существует одна и только одна вершина графа (транспортной сети), в которую входят дуги, но ни одна дуга не выходит. Эта вершина называется стоком сети.

2). Конечный граф без петель называется транспортной сетью, если каждой его дуге 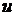отнесено число 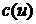, которое может быть как целое, так и дробное. Это число называется пропускной способностью.

3). Пропускная способность дуги 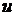транспортной сети может принимать как положительные, так и отрицательные значения.

4). Функция 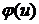, определенная на множестве дуг сети и принимающая произвольные вещественные значения 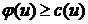, такая, что: 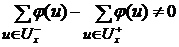– называется потоком.

5). В любой транспортной сети существуют вершины, в которых поток может создаваться и исчезать.

56. Основные понятия и определения теории потоков.

1). Для транспортных сетей определяется понятие: дуговой поток. Это понятие имеет определенные отличия от понятия суммарного потока на конечных дугах, который может быть определен из соотношения .

2). Величина называется суммарным потоком на конечных дугах.

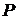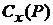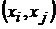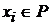3). Для того, что бы получить разрез сети, необходимо все вершины сети разбить на два (возможно и пересекающихся) множества и . Множество дуг , где , а 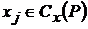образуют разрез.

4). Сумма потоков дуг разреза называется величиной разреза.

5). С изменением разреза величина разреза не меняется.

57. Разрез.

1). Если 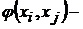Поток дуги 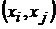, то предполагается, что 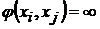, если дуга 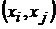не существует.

2). Значение потока на дуге не меньше ее пропускной способности, то есть: .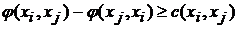

3). Каждую дугу транспортной сети нельзя представлять двумя дугами, имеющими разное направление и, соответственно, два значения потока в прямом и обратном направлениях.

4). В общем случае величина потока на конечных дугах транспортной сети не превышает величину разреза: .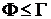

5). Поток и пропускная способность считаются величинами произвольного знака, при этом: .

• < Назад
• Вперёд >