Лекция методы исследования операций
Страница 3 из 6
27. Метод ветвей и границ.
1). Правила ветвления: Выбор целочисленной переменной, значение которой в оптимальном решении ЛП имеет наименьшее дробное значение.
2). Не допускается приписывание целочисленным переменным приоритетов и ветвление по переменной с наибольшим приоритетом.
3). Известно правило выбора вершины задачи ЛП для дальнейшего ветвления, на основе оптимального значения целевой функции: Следует выбирать вершину, не доставляющую оптимальное значение целевой функции. Обоснованием служит то соображение, что допустимая область задачи ЛП с наибольшим значением целевой функции может не содержать целочисленное решение.
4). Реализация этого метода заключается в последовательном ветвлении исходного множества решений на так называемое дерево подмножеств с нахождением решений на всех подмножествах, пока не будет получено искомое. По существу это некоторая процедура перебора всех целочисленных допустимых решений исходной задачи.
5). “Последним пришел – первым обслужен”: для дальнейшего ветвления нельзя выбирать задачу ЛП, решавшуюся последней.
28. Задачи многокритериальной оптимизации.
1). Множество допустимых решений, для которых возможно улучшить одновременно все частные показатели эффективности называют множеством Парето или областью компромиссов.
2). В общем случае эффективные решения всегда эквивалентны друг другу, так, что два оптимальных по Парето решения всегда можно сравнить.
3). Задачи многокритериальной оптимизации возникают тогда, когда имеется несколько целей, которые не могут быть отражены одним критерием. Требуется найти точку области допустимых решений, которая оптимизирует все такие критерии.
4). Область компромиссов всегда выпукла, поэтому в задаче многокритериальной оптимизации допустимо построение некоторого обобщенного критерия эффективности, например, в виде взвешенной суммы частных критериев.
5). Веса в обобщенном критерии эффективности многокритериальной задачи определяются на основе методов экспертных оценок.
ПП 6.3. Методы нелинейной оптимизации.
29. Задачи нелинейной оптимизации.
1). Задача нелинейного программирования в формализованной постановке имеет вид:
 ,
,


Здесь:  и хотя бы одна из
и хотя бы одна из  являются нелинейными.
являются нелинейными.
2). Множество допустимых решений нелинейных задач, всегда выпукло.
3). Множество допустимых решений нелинейных задач имеет конечное число вершин.
4). Локальный экстремум задач нелинейной оптимизации является также и глобальным экстремум, следовательно, решение задачи единственно.
5). Если оптимальное значение целевой функции задачи нелинейной оптимизации ограничено, то, по крайней мере, одна крайняя точка множества допустимых решений является оптимальным решением задачи.
30. Метод множителей Лагранжа.
1). Используя необходимый признак экстремума функции нескольких переменных, имеем нормальную систему нелинейных уравнений:
 .
.
2). Если функции  и
и  непрерывны вместе со своими частными производными первого порядка, то задача нелинейной оптимизации может быть сведена к задаче безусловной оптимизации функции Лагранжа:
непрерывны вместе со своими частными производными первого порядка, то задача нелинейной оптимизации может быть сведена к задаче безусловной оптимизации функции Лагранжа:

3). Любое решение системы:

Не является оптимальным решением в смысле утверждений теоремы Куна-Таккера.
4). Не существует методик, которые бы редуцировали задачу нелинейного программирования к виду, допускающему применение симплекс-метода.
5). Для задач нелинейного программирования, подобно задачам линейной оптимизации, всегда удается построить итерационную процедуру, позволяющую получить точное решение за конечное число шагов.
ПП 6.4. Методы векторной оптимизации.
31. Методы решения задач векторной оптимизации.
Существуют следующие несколько методов решения задач векторной оптимизации (отметьте тот метод, который к задачам многокритериальной (векторной) оптимизации не относятся):
1). Метод выделения главного критерия.
2). Метод лексикографической оптимизации.
3). Метод последовательных уступок.
4). Метод множителей Лагранжа.
5). Человеко-машинные процедуры векторной оптимизации.
32. Методы свертывания векторного критерия в скалярный.
1). В методах свертывания векторного критерия в скалярный исходная задача заменяется задачей:
 ,
,
Где  Скалярный критерий, представляющий собой некоторую функцию относительно компонентов векторного критерия.
Скалярный критерий, представляющий собой некоторую функцию относительно компонентов векторного критерия.
2). Основная проблема построения скалярного критерия – построение функции  , где
, где  Компоненты вектора
Компоненты вектора  . Функция
. Функция  должна быть аналитической (бесконечное число раз дифференцируемой) на всей области определения.
должна быть аналитической (бесконечное число раз дифференцируемой) на всей области определения.
3). Для того чтобы свертка  существовала нет необходимости подтверждать, что показатели эффективности являются однородными.
существовала нет необходимости подтверждать, что показатели эффективности являются однородными.
4). Свертка  показателей из разных групп не приводит к потере физического смысла критерия.
показателей из разных групп не приводит к потере физического смысла критерия.
5). Нормализация критериев (приведение к безразмерным величинам) в задаче построения скалярного критерия не осуществляется.
33. Свертки векторных критериев.
1). Свертка компонентов векторного критерия в виде:  называется мультипликативной.
называется мультипликативной.
2). Свертка компонентов векторного критерия в виде:  называется аддитивной.
называется аддитивной.
3). Способ свертки векторного критерия в скалярный зависит от характера показателей и целей оценивания систем.
4). В мультипликативных критериях схема компромисса предполагает оперирование не с относительными, а с абсолютными изменениями частных критериев.
5). В мультипликативном критерии, как и в аддитивном, требуется нормировка частных критериев.
ПП 6.5. Игровые модели.
34. Общие определения. Классификация моделей игр.
1). Дискретными играми называются игры, в которых множество стратегий дискретно. Дискретная игра может быть только бесконечной.
2). В непрерывных играх множество стратегий непрерывно, представляет собой континуум с конечным числом стратегий.
3). В играх двух лиц с дискретным набором стратегий имеет место платежная функция  , где
, где 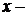 Стратегии первого игрока, а
Стратегии первого игрока, а 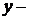 Стратегии второго игрока.
Стратегии второго игрока.
4). В непрерывных играх двух лиц можно строить так называемую платежную матрицу некоторой размерности  .
.
5). Теория игр изучает и рассматривает методы определения оптимальных стратегий управления поведением в системах, для которых характерно наличие конфликтной ситуации, то есть в простейшем случае игры двух лиц кибернетическая модель игры обязательно должна иметь, интересы которых полностью или частично противоположны.
35. Классификация моделей игр.
1). Комбинаторная неопределенность: ставить вопрос об оптимальности или правильности выбора стратегий в таких играх неразумно, так как исход игры не зависит от поведения игроков.
2). Игры различают по характеру множества стратегий или, точнее, по характеру неопределенности игровой ситуации, в которой требуется принимать решение.
3). Случайный тип неопределенности: связан с ситуацией, в которой число исходов игры, стратегий, факторов, определяющих исход игры, конечное, но очень велико.
4). Стратегическая неопределенность: одна играющая сторона знает априорную информацию о поведении противоположной стороны и, в зависимости от этого, строит свою стратегию.
5). Игры  лиц
лиц  делятся на антагонистические и неантагонистические.
делятся на антагонистические и неантагонистические.
36. Классификация моделей игр.
1). Игры в нормальной форме имеют другое название – позиционные игры. Они изображаются в виде графа.
2). В непрерывных играх имеет место комбинаторная неопределенность.
3). Антагонистические и неантагонистические игры встречаются только в играх двух лиц.
4). Нельзя рассматривать непрерывные игры как предельный случай дискретных игр.
5). Понятия антагонистических и неантагонистических игр для непрерывного случая, не аналогичны этим же понятиям для дискретных игр.
37. Классификация непрерывных игр.
1). Широко распространенная форма задания непрерывной игры – динамическая или дифференциальная в виде дифференциальных уравнений, которая является полным аналогом динамических (позиционных) игр.
2). По характеру платежной функции, непрерывные игры классифицируются на выпуклые, полиномиальные и «вырожденные». Эти игры не решаются в чистых стратегиях.
3). Всегда в антагонистических непрерывных играх устанавливается время выполнения действия.
4). В большинстве случаев считается, что игра ведется против «умного» противника, который выбирает худшую для партнера стратегию, поэтому для выбора оптимальной стратегии применяются максиминные критерии.
5). В теории игр не рассматриваются методы определения оптимальных стратегий при условии, что противник совершает ошибку.
38. Матричные игры.
1). При выборе стратегий обоими игроками исключается случай, когда выполняется соотношение:  .
.
2). Матричные игры всегда решаются в смешанных стратегиях.
3). Если седловая точка матричной игры существует, то она единственна.
4). В общем случае, матричная игра определяется платежной матрицей вида:
 .
.
5). Известно, что в играх с полной информацией, все элементы платежной матрицы являются седловыми точками.
39. Чистые и смешанные стратегии.
1). Если в векторе  – вероятностей выбора стратегий первым игроком или
– вероятностей выбора стратегий первым игроком или  – вероятностей выбора стратегий вторым игроком (или обоих вместе), все составляющие равны нулю, кроме одной, то такие стратегии называют смешанными.
– вероятностей выбора стратегий вторым игроком (или обоих вместе), все составляющие равны нулю, кроме одной, то такие стратегии называют смешанными.
2). Выбор стратегии осуществляется случайно, частота появления каждой стратегии выбирается разной. Тогда можно говорить об оптимальных значениях вероятности появления каждой стратегии (ее частоте).
3). Если в платежной матрице игры имеются несколько седловых точек, то игра решается в смешанных стратегиях.
4). При наличии смешанных стратегий следует оперировать платежами, а не их средними значениями (математическими ожиданиями).
5). Ценой игры называют некоторое промежуточное значение выигрышей и проигрышей для каждого из игроков по всем их стратегиям.
40. Теорема о минимаксе.
1). Основная теорема теории игр, теорема о минимаксе, утверждает, что максимин среднего платежа  равен минимаксу среднего платежа, то есть:
равен минимаксу среднего платежа, то есть:  , где
, где  Цена игры.
Цена игры.
2). Из теоремы о минимаксе следует, что существует такая пара стратегий  и
и  , что
, что

Для всех  и
и  .
.
3). Как и для чистых стратегий, в общем случае для любой пары смешанных стратегий имеет место:  .
.
4). В оптимальную смешанную стратегию обязательно входят чистые стратегии.
5). Оптимальная смешанная стратегия, примененная против любой активной стратегии, не всегда дает цену игры.
41. Седловая точка.
Матричная игра задана платежной матрицей:
 .
.
Найдите седловую точку игры, если она есть.
1). 3.
2). 4.
3). 2.
4). Платежная матрица седловой точки не имеет.
5). 1.
42. Цена игры.
Матричная игра задана платежной матрицей:
 .
.
Найдите цену игры.
1). 3.
2). 4.
3). 2.
4). 1.
5).  .
.
43. Процедура выделения активных стратегий.
1). Если  и
и  – две оптимальные смешанные стратегии игрока, то выпуклая оболочка
– две оптимальные смешанные стратегии игрока, то выпуклая оболочка  , где
, где  так же является оптимальной смешанной стратегией игрока.
так же является оптимальной смешанной стратегией игрока.
2). Если осуществить перестановку строк или столбцов (или строк и столбцов) платежной матрицы, то цена игры изменится.
3). Цена игры изменится на величину  , если ко всем элементам платежной матрицы прибавить это число.
, если ко всем элементам платежной матрицы прибавить это число.
4). Если платежная матрица  обладает свойством:
обладает свойством:  для всех
для всех 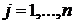 , то говорят, что строка
, то говорят, что строка 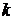 доминирует над строкой
доминирует над строкой  или стратегия
или стратегия  подчинена стратегии
подчинена стратегии 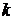 .
.
5). Столбец  строго доминирует над столбцом
строго доминирует над столбцом  , если
, если  для всех
для всех  .
.