Лекция методы исследования операций

Лекция МЕТОДЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ

ПП 6.1. Исследование операций. Общая характеристика.

1. Основные понятия и определения.

1). Операционная модель в самом общем виде может быть представлена уравнением: 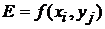, где 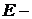Критерий эффективности системы, 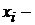Управляемые переменные, 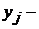Неуправляемые переменны. Ограничения, наложенные на переменные, могут быть выражены в дополнительной системе ограничений (неравенств и уравнений).

2). Один из методов получения оптимального решения – аналитический, состоит в использовании аналитических процедур, основанных на математической индукции.

3). Оценки модели на адекватность могут производиться только ретроспективно с использованием ранее полученных данных.

4). Адекватность решения вытекает из адекватности модели.

5). Решение, полученное на модели, действительно до тех пор, пока управляемые переменные в модели остаются постоянными.

2. Классификация процессов и задач. Процессы создания и хранения запасов.

1). Эти процессы не требуют регулирования запасов.

2). Процессы создания и хранения запасов требуют либо обоих, либо одного из двух следующих решений: (а) сколько заказывать (производить или покупать); (б) когда заказывать.

3). В качестве средств решения задачи управления запасами применяется аппарат условной оптимизации.

4). Процессы создания и хранения запасов являются случайными и здесь основным аппаратом выбора решения, является метод стохастического программирования.

5). Задача управления запасами в общем случае является нелинейной и не может быть редуцирована к задачам линейного программирования.

3. Классификация процессов и задач. Процессы распределения.

1). В процессах распределения, задача не сводится только к соединению операций и ресурсов, таким образом, чтобы добиться оптимального эффекта.

2). Как операции, так и ресурсы в процессах распределения, не задаются в конкретной (окончательной) форме.

3). Процессы распределения возникают, когда (а) существует ряд операций, которые необходимо выполнить, и ряд различных путей их выполнения, (б) нет в наличии ресурсов или средств, обеспечивающих выполнение каждой из этих операций наиболее эффективным образом.

4). Основным инструментом решения задач распределения является условная оптимизация на нечетких множествах.

5). Задача распределения является частным случаем процессов управления запасами.

4. Классификация процессов и задач. Процессы обслуживания.

1). К задачам по определению объема обслуживания и времени появления клиентов (составление расписания) неприменима известная теория очередей в силу детерминированности процесса.

2). В задачах обслуживания объемы и время обслуживания считаются изначально заданными.

3). В задачах обслуживания объемы и время поступления заявок на обслуживание являются случайными величинами.

4). Процессы обслуживания связаны с наличием клиента требующего обслуживания.

5). В задачах распределения порядок обслуживания заявок неважен.

5. Классификация процессов и задач. Процессы замены.

1). К задачам замены оборудования и задачам ремонта не могут быть применены одни и те же методы.

2). Задачи замены оборудования предполагают полную замену, а не ремонт.

3). Процессы замены оборудования, являются строго детерминированными процессами и соответственно к ним применяются только статистические методы.

4). Задачи эксплуатации и ремонта не могут рассматриваться как частный случай задач замены, поскольку здесь требуется, как правило, замена отдельной части, а не всего комплекса оборудования.

5). Процессы замены распадаются на два основных класса в зависимости от вида износа оборудования: либо оно устаревает и далее заменяется, либо оно полностью выходит из строя.

6. Классификация процессов и задач. Состязательные процессы.

1). Игра, как основная из задач состязательных процессов, предполагает наличие только двух игроков, бесконечное множество состояний и нулевую сумму выигрышей обоих сторон.

2). Состязательные процессы – это процессы, в которых эффективность решений одной стороны может оказаться сниженной в связи с решениями другой стороны.

3). В соответствии с теорией игр, всякая игра может быть сведена к задаче линейного программирования и решена симплекс-методом.

4). Частным случаем игры является аукционный торг.

5). В теории торгов предполагается, что число участников ограничено и заранее известно, количество партий неограниченно и эффект стратегии может быть лишь оценен.

ПП 6.2. Методы линейного программирования.

7. Общая задача линейной оптимизации.

1). Общая постановка задачи линейной оптимизации имеет вид:

Требуется обратить в максимум (минимум) целевую функцию

При условиях

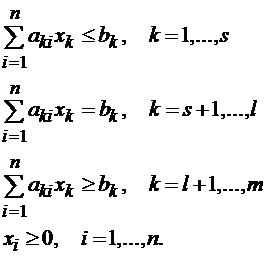
2). Множество всех допустимых планов, образуют область допустимых решений (ОДР) задачи ЛП. Это открытое (не замкнутое) многогранное множество.

3). Область допустимых решений задачи линейного программирования может и не быть выпуклым, поэтому ее нельзя в полном смысле отнести к задачам выпуклого программирования.

4). Решение задачи линейного программирования достигается в крайних точках ОДР, следовательно, если она имеет решение, то это решение единственно.

5). В силу конструктивных особенностей, множество решений задачи линейного программирования непусто.

8. Графический метод решения задачи ЛП.

1). Граница ОДР – объединение отрезков прямых, получаемых из системы ограничений путем замены знаков неравенств на равенства, рассмотренных в первом координатном углу. Внутренняя часть полученного многоугольника определяют ОДР.

2). Прямая линия, параллельная градиенту целевой функции, является геометрическим местом точек, в которых целевая функция принимает одинаковые фиксированные значения. Такие геометрические места точек называют линиями уровня.

3). Для задачи линейной оптимизации градиенты целевой функции – это векторы, координатами которых являются частные производные по переменным задачи. Вектор имеет переменные величину и направление.

4). Графический метод основан на геометрической интерпретации задачи ЛП и эффективно может применяться для решения задач двумерного пространства. Задачи трехмерного пространства этим методом решаются очень редко, так как построение их решения неудобно и лишено наглядности.

5). Движение по линиям уровня целевой функции, вдоль градиента, в направлении противоположном градиенту, приводит к точке максимума целевой функции, в противном случае к – точке минимума.

9. Табличный симплекс-метод.

1). Универсальным вычислительным методом решения задачи ЛП является так называемый симплекс-метод, согласно которому: находясь в одной из вершин многогранной области – из всех соседних вершин выбирается та, которая “улучшает” целевую функцию.

2). Для решения задачи ЛП необходимо предварительно привести математическую модель задачи к каноническому виду: систему активных ограничений типа неравенств ориентировать строго в одном направлении.

3). Весовые коэффициенты при базисных переменных проставляются в нижнюю строку таблицы. Значение целевой функции при текущем базисе

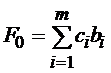
Заносятся в последнюю строку столбца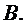

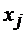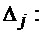
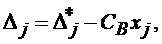
4). Критерий оптимальности: Обозначим относительную оценку небазисной переменной через 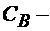Оценки базисных переменных. Если относительные оценки небазисных переменных допустимого базисного решения неотрицательны, то соответствующее решение оптимально.

5). В задаче линейного программирования, решаемой табличным симплекс-методом, начальный допустимый план строится методом потенциалов.

10. Табличный симплекс-метод.

1). Выбор разрешающей строки в симплекс-методе предшествует выбору разрешающего столбца.

2). Критерий выбора разрешающего столбца: минимальный элемент строки .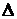

3). В формализованном виде, в канонической форме, задача линейного программирования имеет следующие особенности: целевая функция исследуется на максимум, ограничения преобразуются к уравнениям путем введения искусственного базиса.

4). Критерий выбора разрешающей строки: максимальное из частных от деления элементов столбца 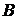на элементы разрешающего столбца.

5). В основе принципов перехода от одной симплекс-таблицы к следующей лежат элементарные преобразования столбцов матрицы системы ограничений.

11. Двойственная задача линейного программирования.

1). Двойственная задача выглядит следующим образом:

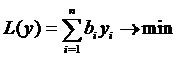
При ограничениях

2). Сопоставляя записи прямой и двойственной задач, можно установить, что, если прямая задача является задачей максимизации, то и двойственная задача, также является задачей максимизации.

3). Коэффициенты целевой функции прямой задачи остаются коэффициентами целевой функции двойственной задачи.

4). Свободные члены ограничений прямой задачи остаются свободными членами ограничений двойственной задачи.

5). Число переменных двойственной задачи равно числу переменных прямой задачи.

12. Соотношения прямой и двойственных задач.

1). Если прямая задача решается на максимум, то в оптимальном решении двойственной задачи

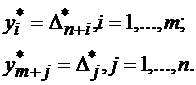
2). Если прямая задача решается на максимум, то в оптимальном решении двойственной задачи

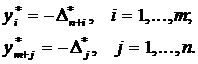
3). Решение прямой задачи получить невозможно, если решать двойственную задачу прямым симплекс-методом.

4). Взаимно однозначное соответствие между переменными исходной задачи и ограничениями двойственной задачи удовлетворяет следующему положению: 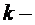Е ограничение двойственной задачи будет неравенством, если на 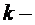Ю переменную исходной задачи наложено требование неотрицательности, если же 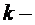Я переменная не ограничена в знаке, то 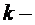Е ограничение будет уравнением.

5). Из существования оптимального решения одной из задач двойственной пары, не следует, что вторая задача вообще имеет решение.

13. Двойственный симплекс-метод.

1). Так же как и прямой симплекс-метод, двойственный симплекс метод является итерационной процедурой, в основе которой лежат элементарные преобразования строк матрицы системы ограничений.

2). Базис пространства переменных двойственной задачи, в котором выполнены все ее, будем называть сопряженным базисом.

3). Если среди компонент разложения вектора 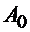по сопряженному базису имеются положительные, то критерий оптимальности не выполнен.

4). В двойственном симплекс-методе выбор разрешающего столбца предшествует выбору разрешающей строки.

5). Значения целевых функций прямой и двойственной задач на оптимальных решениях, вообще говоря, могут не совпадать.

14. Основные утверждения теории двойственности и их экономическое содержание. Первая теорема двойственности.

1). Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование дополнительного плана хотя бы для одной из них.

2). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то это вовсе не значит, что система ограничений другой задачи противоречива.

3). По структуре прямой и двойственной задач (в их канонической постановке), важно отметить, что для любых допустимых планов 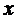и 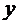(каждой из пары взаимодвойственных задач) справедливо неравенство С экономической точки зрения, это означает, что для любого допустимого плана производства 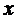и любого допустимого вектора оценок ресурсов 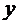общая созданная стоимость не превосходит суммарной оценки ресурсов.

4). Если задача определения оптимального плана, максимизирующей выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукта, не обязательно совпадает с суммарной оценкой ресурсов.

5). Двойственные оценки не гарантируют рентабельность оптимального плана, то есть равенства общей оценки продукции и ресурсов.

15. Вторая теорема двойственности и ее экономическое содержание.

1). Для того, чтобы планы 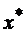и 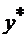Пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:

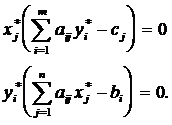
Это условия дополняющей нежесткости.

2). Если какое-либо неравенство системы ограничений одной из задач не обращается в тождество оптимальным планом этой задачи, то соответствующая компонента оптимального плана двойственной задачи не должна равняться нулю

3). Если какая-либо компонента оптимального плана одной из задач отрицательна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в тождество.

4). Если по некоторому оптимальному плану 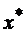производства, расход 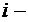Го ресурса строго меньше его запасов 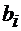, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса отлична от нуля.

5). Если в некотором оптимальном плане оценок его 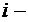Я компонента отрицательна, то в оптимальном плане производства расход соответствующего ресурса равен его запасу.

• < Назад
• Вперёд >