Задачи Квадратичное программирование (примеры)
Задачи Квадратичное программирование (примеры)
Пример 1. Рассмотрим задачу
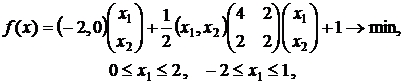
Очевидно, что целевая функция квадратичная и выпуклая 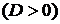 .
.
Найдем стационарную точку X* 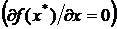 . Поскольку
. Поскольку 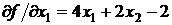 ,
, 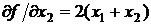 , то
, то 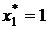 ,
, 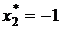 . Вектор X* оказался планом задачи и, значит, X* — оптимальный план.
. Вектор X* оказался планом задачи и, значит, X* — оптимальный план.
Решим задачу релаксационным методом, иллюстрируя его операции геометрически. Возьмем качестве начальном точку 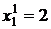 ,
, 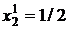 . Построим на плоскости
. Построим на плоскости 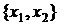 прямые
прямые 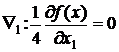 ,
, 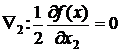 . Поскольку в релаксационном методе каждая компонента очередного приближения связана с одномерной минимизацией, то при вычислении
. Поскольку в релаксационном методе каждая компонента очередного приближения связана с одномерной минимизацией, то при вычислении 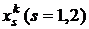 будем двигаться в множестве X параллельно оси
будем двигаться в множестве X параллельно оси 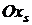 по направлению к прямой
по направлению к прямой 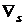 до полной релаксации функции F по 1-ой компоненте. Поэтому геометрически построение релаксационным методом последовательности
до полной релаксации функции F по 1-ой компоненте. Поэтому геометрически построение релаксационным методом последовательности 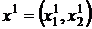 ,
, 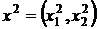 выглядит так, как это изображено на рис.__ Из него видно, что за конечное число итераций оптимальный план X° построить не удается.
выглядит так, как это изображено на рис.__ Из него видно, что за конечное число итераций оптимальный план X° построить не удается.
Ту же целевую функцию F(X) на множествах
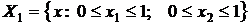 ,
,
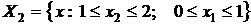
Релаксационный метод минимизирует за конечное число итераций.