Матричные транспортные задачи Мтз (задания)
Матричные транспортные задачи Мтз (задания)
ЗАДАНИЯ
4.1. Составить план перевозки зерна из районов A1—A4, в которых запасы составляют Ai Тыс. ц Зерна (данные приведены в табл. 4.11Б), на пять элеваторов B1—B5 мощностью в Тыс. Ц (данные приведены в табл. 4.11В) с минимальными издержками на перевозку. Затраты на перевозку 1 Ц зерна заданы в табл. 4.11А ( в Тыс. д. е.).
1. Начальный план перевозок составить по правилу северо-западного угла и по правилу минимального элемента. Определить какой из планов ближе к оптимальному. Решить задачу, исходя из последнего начального плана перевозок.
2. Решить задачу также в следующих случаях:
А) Запасы четвертого района на 2 Тыс. ц зерна меньше указанных в табл. 4.11Б.
Б) Мощность пятого элеватора на 3 Тыс. ц меньше указанной в табл. 4.11В.
В) Невозможность доставки зерна из второго района к третьему элеватору.
Г) С обязательной поставкой зерна из 3-го района на 3-й элеватор в количестве 1 Тыс. ц зерна и обязательной поставкой первым районом второму элеватору не менее 2 Тыс. ц зерна.
Д) Невозможность поставки зерна из четвертого района к пятому элеватору более 2 Тыс. ц зерна.
Табл. 4.11А. Матрицы тарифов
|
1.
|
10 8 5 9 16
4 3 4 11 12
5 10 29 7 6
9 2 4 1 3
|
2.
|
10 7 2 4 5
8 4 3 7 3
2 4 10 11 8
8 12 9 7 6
|
3.
|
3 9 11 8 11
6 2 3 6 5
10 4 13 8 10
3 8 7 5 7
|
|
4.
|
10 10 5 1 5
4 10 2 10 2
10 8 10 5 2
4 2 10 10 8
|
5.
|
6 2 10 4 10
2 1 1 9 10
5 2 10 10 7
10 5 10 4 8
|
6.
|
8 10 8 10 4
3 10 1 6 1
10 9 10 8 3
1 12 10 1 10
|
|
7.
|
3 4 10 10 3
9 10 7 7 10
9 8 10 8 10
2 10 8 10 9
|
8.
|
10 1 3 10 2
10 8 3 10 2
10 2 16 10 8
7 10 10 5 3
|
9.
|
10 6 10 7 3
2 10 1 9 10
2 3 15 10 10
10 5 10 6 5
|
|
10.
|
3 9 10 10 2
7 10 1 3 3
9 10 10 1 3
10 6 1 10 6
|
11.
|
3 4 10 2 10
3 6 4 10 10
10 7 8 10 4
10 4 1 2 10
|
12.
|
10 5 10 9 6
1 10 2 2 10
10 5 12 10 1
10 9 3 3 10
|
|
13.
|
10 10 1 2 9
10 6 1 5 3
10 8 14 5 10
9 10 2 6 10
|
14.
|
10 4 8 6 10
10 2 3 10 3
7 10 10 2 3
10 3 2 10 1
|
15.
|
4 6 8 10 2
3 4 3 9 5
4 6 13 2 1
2 3 4 10 9
|
|
16.
|
8 5 8 2 7
9 2 3 10 9
16 12 12 8 14
10 6 3 6 12
|
17.
|
9 10 16 4 12
13 1 2 1 9
2 20 12 8 4
30 10 10 14 18
|
18.
|
3 10 6 10 10
10 2 1 8 12
16 10 15 10 10
9 14 10 10 10
|
|
19.
|
10 8 3 8 5
10 5 2 1 14
10 12 20 13 20
6 2 16 3 18
|
20.
|
10 6 14 16 7
8 3 3 8 5
12 20 14 20 10
10 5 18 16 4
|
21.
|
1 3 4 7 5
10 8 1 2 3
8 10 14 6 8
7 5 9 12 11
|
|
22.
|
3 5 11 8 10
8 7 1 4 3
10 11 12 9 7
6 4 7 8 10
|
23.
|
4 5 8 7 5
5 10 1 11 8
3 4 8 7 1
2 10 11 10 4
|
24.
|
3 5 7 5 4
10 12 1 4 8
10 11 10 8 7
10 8 9 7 8
|
|
25.
|
10 3 8 11 2
8 7 6 10 5
11 10 12 9 10
12 14 10 14 8
|
26.
|
10 1 7 2 4
8 3 2 2 10
5 2 6 2 2
10 3 2 4 2
|
27.
|
11 12 13 14 15
6 7 6 9 10
1 2 5 4 5
17 15 19 12 11
|
|
28.
|
1 2 3 6 5
6 7 3 9 10
1 2 5 4 5
6 7 8 9 2
|
29.
|
1 5 9 3 6
2 6 5 4 7
3 7 16 5 8
4 8 12 6 2
|
30.
|
6 8 4 10 10
10 12 1 8 9
12 13 13 5 4
2 4 8 6 9
|
|
Табл. 4.11Б. Ресурсы районов
|
Табл. 4.11В. Потребности элеваторов
|
Районы
№ вар.
|
A1
|
A2
|
A3
|
A4
|
|
Элевато-ры
№ вар.
|
B1
|
B2
|
B3
|
B4
|
B5
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
17
11
24
11
20
11
7
17
20
9
21
14
20
8
20
8
8
16
9
10
9
10
11
9
10
7
14
8
10
20
|
8
23
10
11
20
9
31
11
11
27
9
9
10
24
12
10
9
9
8
11
9
10
13
15
25
10
10
13
25
20
|
10
5
21
12
9
11
5
9
9
5
6
6
14
7
6
9
10
8
8
8
6
8
12
25
20
9
10
21
12
15
|
9
15
9
14
16
9
10
13
10
9
10
15
10
10
10
10
11
10
12
9
12
11
18
21
22
12
10
16
24
10
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
6
5
9
17
13
5
5
5
6
10
6
5
6
10
19
6
8
16
6
6
5
12
6
13
20
6
10
8
10
10
|
15
10
10
5
20
8
20
17
15
16
6
8
8
10
10
6
6
6
7
6
6
5
8
12
15
5
6
10
11
17
|
7
11
10
7
7
12
8
16
11
7
10
7
20
8
7
8
9
8
9
8
8
8
17
15
20
8
10
10
15
20
|
8
8
15
11
5
6
11
5
7
7
12
14
5
11
5
9
8
6
8
7
7
6
11
10
12
10
7
10
15
8
|
8
20
20
8
20
9
9
7
11
10
12
10
15
10
7
8
7
7
7
11
10
8
12
14
10
9
11
20
20
10
|
4.2. Для обогрева помещений используют 4 агрегата, каждый из которых может работать на любом из пяти сортов топлива, имеющемся в количествах, указанных в табл. 4.12В (в Десятках тонн). Потребность в топливе каждого из агрегатов (в Десятках тонн) задана в табл. 4.12Б. Теплотворная способоность каждого сорта топлива при использовании его на различных агрегатах определяется матрицей, заданной в табл. 4.12А (количество тепловой энергии, выделяемой при сжигании 1 Т топлива). Найти такое распределение топлива между агрегатами, при котором получается максимальное количество теплоты от использования всего топлива.
А) Составить математическую модель задачи.
Б) Построить начальный план по правилам минимального элемента и двойного предпочтения. Сравнить, какой из них ближе к оптимальному.
В) Решить задачу.
Г) Проверить, является ли оптимальный план единственным. Если — нет, построить другой оптимальный план.
Табл. 4.12А. Матрицы теплотворной способности топлива
|
1.
|
4 5 10 11 1
3 5 3 10 11
12 14 15 10 11
2 5 6 7 10
|
2.
|
1 4 5 7 8
10 11 12 8 7
11 8 10 4 5
7 6 10 2 2
|
3.
|
1 6 5 7 5
10 8 3 4 5
8 7 8 5 10
7 8 7 6 5
|
|
4.
|
2 5 8 7 6
5 3 4 8 9
10 11 10 12 10
6 9 10 9 10
|
5.
|
1 3 5 8 7
6 9 10 11 8
7 10 11 9 6
5 4 6 8 10
|
6.
|
1 6 8 6 15
9 3 4 5 8
8 9 10 10 9
8 7 6 5 10
|
|
7.
|
1 6 5 6 7
8 9 10 11 10
10 9 6 7 8
8 10 2 4 5
|
8.
|
10 10 3 10 10
8 4 2 3 10
5 1 10 6 10
10 7 10 10 8
|
9.
|
10 2 10 6 3
8 10 2 10 10
2 8 10 4 2
8 2 6 2 6
|
|
10.
|
8 12 6 8 14
12 1 16 10 6
2 9 16 6 20
16 18 1 2 4
|
11.
|
3 14 14 4 16
9 10 12 20 12
10 1 8 9 2
6 10 1 12 14
|
12.
|
20 14 14 4 16
12 10 12 20 12
1 10 8 9 2
6 10 1 12 14
|
|
13.
|
14 20 13 5 12
3 2 16 11 20
15 7 17 4 12
9 8 18 19 1
|
14.
|
45 55 60 40 20
50 30 20 20 15
35 20 85 10 10
75 10 15 95 50
|
15.
|
1 3 10 2 10
5 10 1 10 6
10 4 10 7 10
10 10 9 8 10
|
|
16.
|
10 9 7 6 18
11 8 5 19 17
12 13 3 4 16
1 20 2 14 15
|
17.
|
6 10 10 8 9
5 4 5 2 10
4 6 1 11 12
4 2 4 13 4
|
18.
|
12 10 12 11 10
10 12 10 11 12
6 7 8 10 9
5 4 1 3 2
|
|
19.
|
2 4 8 9 4
5 3 3 7 8
9 6 4 2 6
10 10 6 3 5
|
20.
|
2 14 14 8 2
16 4 6 12 10
2 4 6 12 10
2 4 18 8 6
|
21.
|
1 2 5 6 7
10 10 8 4 3
5 4 3 3 5
7 9 8 7 2
|
|
22.
|
4 1 2 3 7
8 6 7 6 8
5 9 10 10 3
10 11 6 5 8
|
23.
|
1 5 2 6 4
6 7 8 7 9
6 5 5 5 4
10 10 11 10 9
|
24.
|
1 4 5 6 7
5 6 5 4 3
10 6 5 7 2
7 8 8 10 1
|
|
25.
|
1 5 4 3 2
8 6 5 5 7
6 5 4 4 3
8 6 10 10 9
|
26.
|
2 4 5 5 6
7 8 6 5 2
5 10 10 6 1
6 7 8 9 3
|
27.
|
4 3 1 7 1
6 8 2 10 3
11 10 8 5 2
5 5 8 4 3
|
|
28.
|
3 2 5 4 3
10 8 7 6 8
7 8 5 4 4
5 4 8 10 6
|
29.
|
1 5 4 3 7
8 6 5 7 2
6 7 2 4 3
5 10 10 7 6
|
30.
|
1 3 2 8 2
6 5 5 3 1
5 2 2 1 4
4 5 7 8 6
|
|
Табл. 4.12Б. Потребности агрегатов в
Топливе
|
Табл. 4.11В. Наличие сортов топлива
|
№ агре-гата
№ вар.
|
1
|
2
|
3
|
4
|
|
№ сорта топлива
№ вар.
|
1
|
2
|
3
|
4
|
5
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
8
10
6
3
8
6
15
6
30
4
10
15
17
22
5
11
8
13
15
16
10
10
8
12
6
10
10
8
1
1
|
9
17
7
10
15
8
18
4
5
8
6
7
8
6
10
11
8
15
35
21
18
15
10
12
8
15
20
8
9
9
|
7
6
12
11
14
10
22
2
25
14
4
5
4
44
6
11
7
5
60
8
14
11
11
8
6
15
15
8
8
9
|
16
17
15
11
11
14
14
6
120
15
5
8
5
20
8
8
8
6
40
11
8
8
12
8
10
10
25
6
8
5
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
14
10
6
3
8
6
15
5
20
7
9
5
10
26
2
8
6
9
10
8
6
4
1
10
5
20
14
5
3
2
|
6
8
8
7
10
5
17
4
40
8
4
11
8
9
4
12
6
9
20
12
9
8
5
5
5
4
26
5
3
5
|
10
9
14
6
5
5
17
2
5
9
3
9
5
8
10
10
7
8
30
10
10
12
15
1
10
16
10
10
5
5
|
2
13
4
5
6
12
4
3
60
7
2
6
6
44
4
5
6
7
40
12
18
6
14
10
5
5
5
5
5
4
|
8
10
8
14
19
10
16
4
55
10
7
4
5
5
9
6
6
6
50
14
7
14
6
5
5
5
15
5
10
8
|
4.3. Решить задачу 4.1 п.1 с прямыми ограничениями на перевозки, определенных матрицами 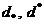 :
: