Лекція Методи розрахунку електродинамічних зусиль (е. д. з.)
Страница 1 из 3
Лекція Методи розрахунку електродинамічних зусиль (е. д. з.)
Якщо елементарний провідник DL зі струмом І Знаходиться в магнітному полі з індукцією В, що створюється другим провідником, то сила DF, Що діє на цей елемент, рівна:
 DF = i [dlB] = i B dl sinB,
DF = i [dlB] = i B dl sinB,
Де І – струм; B – кут між векторами елемента Dl і індукції В, Що вимірюється кутом повороту вектора Dl до вектора В По найкоротшій відстані. За напрямок Dl приймається напрямок струму в елементі. Напрямок індукції В, що створюється другим провідником, визначається за правилом буравчика, а напрямок сили – по правилу лівої руки.
Для визначення повної сили, що діє на провідник довжиною L, необхідно просумувати сили. діючі на всі його елементи:
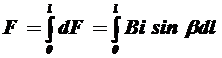 , (1.1)
, (1.1)
У випадку будь-якого розташування провідників в одній площині b=90° І рівняння спрощується:
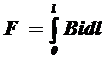 , (1.2)
, (1.2)
Описаний метод рекомендується застосовувати тоді, коли можна аналітично знайти індукцію в будь-якій місці провідника, для якого необхідно визначити силу. Індукцію визначають, використовуючи закон Био — Саварра-Лапласа, відомий з курсу теоретичних основ електротехніки. Другий метод заснований на використанні енергетичного балансу системи провідників зі струмом. Якщо зневажити електростатичною енергією системи і прийняти, що при деформації струмоведучих чи контурів при їхньому переміщенні під дією е. д.з. величина струму у всіх контурах залишається незмінної, то силу можна знайти по рівнянню
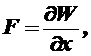 (1.3)
(1.3)
Де W— електромагнітна енергія;
X — можливе переміщення в напрямку дії сили.
Таким чином, сила дорівнює частинної похідної від електромагнітної енергії даної системи по координаті, у напрямку якої діє сила.
Електромагнітна енергія системи обумовлена як енергією магнітного полючи кожного ізольованого контуру, так і енергією, обумовленою магнітним зв'язком між контурами, і для двох взаємозалежних контурів дорівнює:
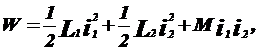 (1.4)
(1.4)
Де L1 і L2 — індуктивності контурів; І 1 і І 2 — струми, що протікають у них; М — Взаємоіндуктивність.
Перші два члени рівняння визначають енергію незалежних контурів, а третій член дає енергію, обумовлену їх магнітним зв'язком.
Рівняння (1.4) дає можливість розрахувати як сили, що діють в ізольованому контурі, так і силу взаємодії контуру з всіма іншими.
Для визначення сил усередині одного незалежного контуру користаємося рівнянням
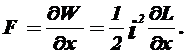 (1.5)
(1.5)
При розрахунку сили взаємодії контурів ми вважаємо, що енергія міняється тільки в результаті зміни взаємного розташування контурів. При цьому енергія, обумовлена власною індуктивністю, вважається незмінною. У даному випадку сила взаємодії між контурами дорівнює:

Енергетичний метод зручний, коли відома аналітична залежність індуктивності; чи взаємоіндуктивності від геометричних параметрів. З рівняння (1.3) випливає, що позитивному напрямку сили F відповідає зростання енергії системи 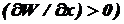 .
.
Електромагнітна енергія одного контуру дорівнює:
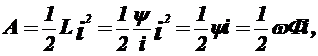
Де Y — потокощеплення; Ф — потік; W — Число витків у контуру.
Сила, що діє в контурі, буде спрямована таким чином, щоб індуктивність, потокощеплення і потік при деформації контуру під дією цієї сили зростали.
1.3 РОЗРАХУНОК СИЛ МІЖ РІВНОБІЖНИМИ ПРОВІДНИКАМИ
Розглянемо спочатку задачу для нескінченно тонких провідників кінцевої довжини мал. 1-1,а. У цьому випадку легко аналітично знайти індукцію в будь-якій місці простору. Тому для визначення сили скористаємося першим методом.
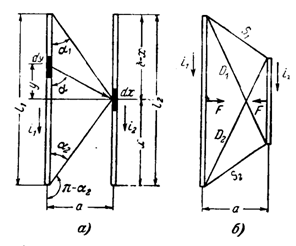
Рисунок 1.1
Відповідно до закону Био—Саварра—Лапласа елементарна індукція від елемента струму I1dy у місці розташування елемента Dx дорівнює:
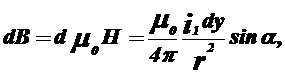 (1.6)
(1.6)
Де M0 — магнітна проникність повітря, рівна 0,4p10-6 Гн/м; а — кут між струмом I1 і променем R від Dy до розглянутого елемента Dx. Повна індукція від провідника L1 у тій місці, де розташований елемент Dx, дорівнює:
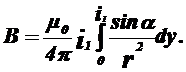 (1.7)
(1.7)
Перейдемо до нової змінної
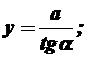
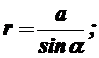
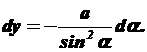
Після підстановки Y ,r і Dy у (1.7) одержимо:
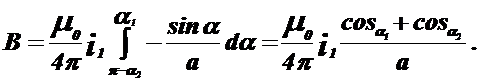 (1.8)
(1.8)
Сила взаємодії між провідником L1 і елементом Dx
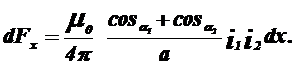 (1.9)
(1.9)
Для визначення повної сили, що діє на провідник L2, Підставимо (1.8) у (1.1).
Змінною інтегрування тепер є Х — координата на провіднику L2. Кути A1 і A2 для кожної крапки Х виражаються в такий спосіб:
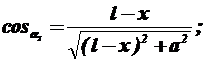

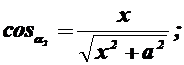
Тоді
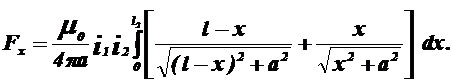
Якщо L1=L2=L , То
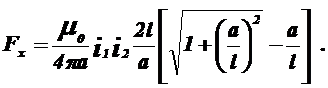 (1.10)
(1.10)
Добуток 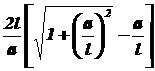 залежить тільки від розмірів провідників і їхнього розташування. Назвемо його геометричним фактором. Тоді
залежить тільки від розмірів провідників і їхнього розташування. Назвемо його геометричним фактором. Тоді
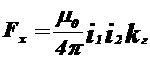 (1.11)
(1.11)
Якщо відстань між провідниками значно менше їхньої довжини А/l«L, то Kг можна прийняти рівним 2l/a (випадок нескінченно довгих шин). При А/l£0,1 розрахунок по формулі
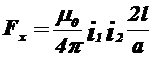 (1.12)
(1.12)
Дає похибку не більш 5% (убік збільшення). Для двох рівнобіжних провідників різної довжини, розташованих з будь-яким зрушенням. Г. Б. Холявский одержав зручну для розрахунку формулу (мал. 1-1,Б)
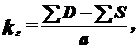 (1.13)
(1.13)
Де SD — сума діагоналей трапеції, побудованої на взаємодіючих провідниках; SS — сума бічних сторін цієї трапеції; А — відстань між провідниками.
При перебуванні електродинамічних сил ми вважали, що перетин провідників нескінченно малий і весь струм йде по їх геометричній осі.
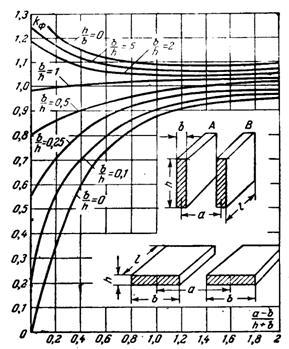
Рисунок 1.2
У дійсності перетин провідників завжди звичайно. Можна показати, що для провідників круглого і трубчастого перетину форма перетину не робить впливу на величину електродинамічної сили. У цьому випадку при розрахунках можна прийняти, що струм йде по геометричній осі.
Для шин прямокутного перетину форма перетину впливає на величину електродинамічної сили. У цьому випадку можна користатися рівнянням (1.11) з урахуванням форми перетину провідника:
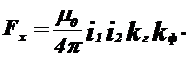
Криві для коефіцієнта форми Kф приведені на рисунку 1.2.
1.4 РОЗРАХУНОК СИЛ І МОМЕНТІВ, ЩО ДІЮТЬ НА ПЕРЕМИЧКУ
В електричних апаратах дуже часто зустрічається розташування частин струмоведучого контуру під прямим кутом (мал. 1.3,а). Заради спрощення задачі, при розрахунку приймаємо, що струм тече по геометричній осі провідників і вертикальний провідник іде в нескінченність.
Сила, що діє на елемент перемички Dx, дорівнює:
DFx = iBxdx.
Індукція Вх Від напівнескінченного провідника в місці на відстані Х Від його осі дорівнює:
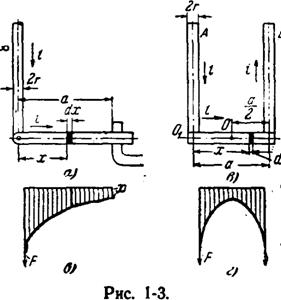
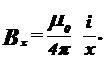 (1.14)
(1.14)
Зазначений закон зміни індукції справедливий у всіх крапках простору, за винятком Х<r . Тоді повна сила Fx, що діє на перемичку на довжині від R до А, Буде дорівнювати:
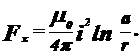 (1.15)
(1.15)
Оскільки довжина вертикального провідника скінченна, то індукція в дійсності менше, ніж це випливає з рівняння (l.14), a реальна сила, що діє на перемичку, менше, ніж дає рівняння (1.15).
Розподіл сили уздовж перемички представлене на мал. 1-3,б. В міру видалення від осі вертикального провідника індукція зменшується, що веде до зменшення сили.
Облік форми перетину струмоведучих провідників у розглянутому випадку дуже складний. Так само як і для рівнобіжних провідників, існують спеціальні криві, що дозволяють врахувати форму перетину провідників.
У масляних вимикачах і інших апаратах струмоведучий ланцюг може мати вигляд «петлі» (мал. 1-3,В). На перемичку в цьому випадку діє сила як від правого, так і від лівого вертикального провідників, тобто сила буде вдвічі більшої той, котру одержуємо по формулі (1.15). Якщо «петля» виконана з провідників круглого перетину, то силу можна знайти, скориставшись енергетичним методом.
Відомо, що індуктивність П-подібної петлі дорівнює:
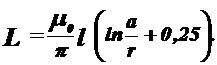 (1.16)
(1.16)
Диференціюючи (1.16) по L І підставляючи в (1.5), отримаємо:
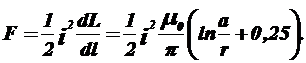 (1.17)
(1.17)
Формула (1.17) враховує і силу, що виникає в місці переходу струму з одного провідника в іншій.
При розрахунку електродинамічної стійкості необхідно визначати момент е. д.з. щодо місця обертання рухливого контакту або щодо місця кріплення. Розрахуємо згинаючий момент, створюваний е. д.з. у місці Об кріплення траверси до тяги мал. 1-3,в. При висновку покладемо, що вертикальні провідники нескінченні і що струм проходить по їх геометричній осі.