Навчальний посібник Автоматизація технологічних процесів і систем автоматичного керування (частина 1)

ЗАПИТАННЯ

1. Що може бути Об'єктами автоматизації у сільському господарстві? 2. Що Дозволяють визначити властивості об'єкта управління? 3. Як записується Закони збереження для теплових об'єктів, для об'єктів, що здійснюють круговий та лінійний рух при аналітичному методі дослідження об'єктів? 4. Які Переваги аналітичного методу дослідження об'єктів автоматизації? 5. В чому Полягає графічна апроксимація? 6. Які переваги мЕтоду інтегральних площин? 7. Як визначається Передаточна функція за умов пасивного експерименту об'єкт управління?

ТЕСТИ

1. Що називається об’єктом автоматизації під час Розробки систем автоматизації?

A. Будь-який технологічний процес, машина, устаткування, апарат, що підлягає автоматизації.

B. Будь-який технологічний процес, що підлягає автоматизації.

C. Будь-яка машина, устаткування, апарат, що підлягає автоматизації.

2. Де Забезпечуються найбільш сприятливі умови для автоматизації?

A. Для переробки та зберігання сільськогосподарської продукції.

B. Для стаціонарних процесів у тваринництві, закритому ґрунті, переробці та зберіганні сільськогосподарської продукції.

C. Для стаціонарних процесів у тваринництві, мобільної техніки.

3. Як Класифікуються об'єкти автоматизації?

A. Прості та складні.

B. Прості та складні; із зосередженими та розподіленими параметрами.

C. Зосередженими та розподіленими параметрами.

4. Скількома Координатами описуються динамічні властивості простого об'єкта автоматизації?

A. За допомогою двох узагальнених (входу та виходу) координат.

B. Потребує не менше трьох координат.

C. За допомогою чотирьох узагальнених (входу та виходу) координат.

5. Скількома Координатами описуються динамічні властивості складного об'єкта автоматизації?

A. За допомогою двох узагальнених (входу та виходу) координат.

B. Потребує не менше двох координат.

C. Потребує не менше трьох координат.

6. Вкажіть Рівняння А. Стодоли, яке використовується для визначення передаточних функцій об'єктів.

А. S 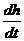=ΣQ,

Де S – площа основи резервуарів; h – рівень рідини; Q – потоки рідин.

В. Та ± δу = Δх,

де Та – час розгону об'єкту; δ – коефіцієнт самовирівнювання; Δх, Δу – відхилення змінних на вході та виході об'єкту.

С. L 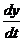= х,

де х, у – вхід та вихід об'єкта; L – незмінні його властивості.

7. Як Поділяються залежно від знаку коефіцієнта самовирівнювання об'єкти автоматизації?

А. δ >0 статичні стійкі; δ = 0 астатичні; δ <0 статичні нестійкі.

В. δ >0 статичні стійкі; δ <0 статичні нестійкі.

С. δ >0 статичні стійкі; δ = 0 астатичні.

8. Який Вигляд має передаточна функції для астатичного об'єкту?

А. ε = = .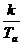

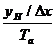В. W(р) = .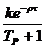

С. W(р) = 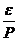Е-ρτ, де ε – швидкість розгону об'єкту

9. Який Вигляд має передаточна функції для статичного об'єкту?

А. W(р) = .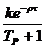

В. ε = = .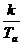

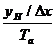С. W(р) = 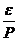Е-ρτ.

10. Як Розраховується швидкість розгону об'єкта?

А. W(р) =

В. ε = = .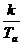

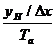С. W(р)= 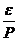Е-ρτ.

1.6. ВИБІР АЛГОРИТМУ УПРАВЛІННЯ ОБ'ЄКТОМ

Динамічні властивості об'єктів управління дають змогу розробникам систем автоматики на стадії проектування визначити алгоритм управління. Для цього слід проаналізувати співвідношення між постійною часу та часом запізнювання. Відомо, що

0,2 ≤ ≤ 1 — безперервний (лінійний),

< 0,2 — позиційний,

> 1—рекомендують імпульсний алгоритм управління.

При визначенні алгоритму управління необхідно пам'ятати, що структура передаточної функції повинна відповідати виразам для статичного і астатичного об’єкту. Метод інтегральних площин дає більш складну структуру. У цьому випадку:

За передаточною функцією знаходять оригінал, за яким будують криву розгону;

Крива розгону (побудована) апроксимується графічним способом, яких би динамічних властивостей не мали зазначені об'єкти;

Розраховані параметри передаточної функції використовуються для визначення алгоритму управління.

Лінійний алгоритм управління — один із найпоширеніших у сільськогосподарському виробництві. Він поєднує пропорційний, інтегральний, пропорційно-інтегральний, пропорційно-диференційований, пропорційно-інтегрально-диференційований. Кожний з них має свої недоліки і а переваги.

У практиці проектування для конкретного об'єкту вибирають такий алгоритм, який би забезпечив один із трьох типових перехідних процесів: аперіодичний, з 20 % перерегулюванням та з мінімальним інтегральним показником якості (рис. 1.23). Аперіодичний характеризується максимальним динамічним відхиленням, мінімальним часом регулювання та відсутністю перерегулювання. Перехідний процес з 20 % перегулюванням середній по якості. Перехідний процес з мінімальним інтегральним показником якості (площа між кривою перехідного процесу та віссю часу мінімальна) характеризується значним перерегулюванням, найбільшим часом регулювання та мінімальним динамічним відхиленням. Конкретний типовий перехідний процес може бути визначений з урахуванням вимог технологів до відповідного об'єкту управління.

Методика вибору найкращого алгоритму управління полягає у визначенні динамічного коефіцієнта регулювання. Для статичних об'єктів:

Rд =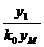

Де у1 – максимальне динамічне відхилення; kо – коефіцієнт передачі об'єкта управління; ум – максимально можливе збурення по навантаженню (у відсотках переміщення регулюючого органу).

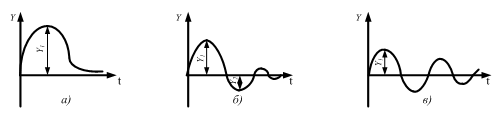
Рис. 1.23. Типові перехідні процеси:

А – Аперіодичний; б – Із 20 %- ним перерегулюванням; в – Із мінімальним інтегральним показником якості

Після цього за графічними залежностями визначають алгоритм управління.

Таблиця 1.18 Динамічні коефіцієнти регулювання для астатичних об’єктів

Алгоритм управління	Динамічні коефіцієнти регулювання
Аперіодичний	Із 20% - ним перерегулюванням	Із мінімальним інтегральним критерієм
Пропорційний Пропорційно-інтегральний Пропорційно-інтегрально - диференціальний	2,9 1,4 1,3	1,4 1,3 1,1	- 0,9 0,8

Для астатичних об'єктів:

Rд =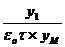

Де εо — швидкість розгону об'єкта; τ — час запізнювання.

Для астатичного об'єкта алгоритм управління знаходять за табл. 1.18.

Для того, щоб переконатись у правильності вибору алгоритму управління, розраховують час регулювання, який потім порівнюють із вимогами технологів:

Tр = τφ,

Де φ— відносний час регулювання, що вибирається за табл. 1.19.

Позиційний алгоритм управління — найдешевший, але придатний лише для низькочастотних об'єктів, тобто для тих, що пропускають тільки першу гармоніку. На відміну від лінійних алгоритмів позиційний потребує для розрахунків параметрів настройки регуляторів не метод синтезу, а метод аналізу. Широке застосування при цьому отримав метод Гольдфарба, в основі якого лежить метод гармонічної лінеаризації.

Таблиця 1.19 Відносний час регулювання

Алгоритм управління	Об’єкт	Відносний час регулювання
Аперіо- Дичний	Із 20% - ним перерегулю-ванням	Із мінімальним інтегральним критерієм
Пропорційний Пропорційно-інтегральний Пропорційно-інтегрально-диференціальний	Статичний Астатичний Статичний Астатичний Статичний Астатичний	4,5 6,0 8,0 14,0 5,5 9,0	6,5 8,0 12,0 16,0 7,0 12,0	9,0 - 16,0 18,0 10,0 13,0

Застосування методу гармонічної лінеаризації передбачає деяку нелінійну ланку, що входить до складу системи автоматизації, замінити лінійною, властивості якої характеризуються коефіцієнтами гармонічної лінеаризації:

Wн(р) = gi+ 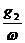Р,

Де g1, g2 – коефіцієнт гармонічної лінеаризації.

Розрахунок параметрів настройки полягає в тому, що розробники задаються деякою зоною нечутливості і розраховують параметри автоколивань, що виникають в системі. Якщо вони відповідають вимогам технологів, то розрахунки на цьому завершують. Якщо ж ні, то беруть інші значення зони нечутливості і так доти, доки не отримують задовільний результат.

ЗАПИТАННЯ

1. Що дають дИнамічні властивості об'єктів управління розробникам систем автоматики? 2. Яка послідовність Визначення алгоритму управління методом інтегральних площин? 3. Чим Характеризується перехідний процес із 20 %- ним регулюванням? 4. Як Визначається динамічний коефіцієнт регулювання для статичних об'єктів? 5. Як Визначається динамічний коефіцієнт регулювання для астатичних об'єктів? 6. Яким Метод застосовують для позиційного алгоритму управління?

ТЕСТИ

1. Які види Управління поєднує лінійний алгоритм управління

A. Пропорційний, інтегральний, пропорційно-інтегрально-диференційований.

B. Пропорційний, інтегральний, пропорційно-інтегральний, пропорційно-диференційований, пропорційно-інтегрально-диференційований.

C. Пропорційний, пропорційно-інтегральний, пропорційно-диференційований.

2. Чим Характеризується аперіодичний перехідний процес?

A. Максимальним динамічним відхиленням, мінімальним часом регулювання та відсутністю перерегулювання.

B. Найбільшим часом регулювання та мінімальним динамічним відхиленням.

C. Середній за якістю перехідний процес.

3. В чому Полягає розрахунок параметрів настройки?

A. Задаються деякою зоною нечутливості, що виникають в системі.

B. Розраховують параметри автоколивань, що виникають в системі.

C. Задаються деякою зоною нечутливості і розраховують параметри автоколивань, що виникають в системі.

1.7. АНАЛІЗ ПАРАМЕТРІВ АВТОМАТИЧНОЇ СИСТЕМИ КЕРУВАННЯ

1.7.1. Стійкість системи та методики перевірки

Одним з основних показників, що характеризують автоматичну систему, є її стійкість.

Стійкість — це властивість системи повертатися в початковий стан після припинення дії обурення.

Нестійка система не повертається в стан рівноваги. Вихідна величина такої системи безперервно збільшується або скоює неприпустимо великі коливання.

Тому, такі системи не придатні для практичного використовування. Російський вчений А. М. Ляпунов запропонував оцінювати стійкість автоматичних систем на основі аналізу рівняння динаміки даної системи.

Для визначення стійкості системи необхідно розв’язати рівняння системи, записане в операторній формі і визначити значення кореня рівняння. Якщо всі корені мають негативну дійсну частину, то система буде стійкою. Якщо дійсна частина хоча б одного кореня рівна нулю, а дійсні частини інших коренів негативні, то система знаходиться на межі стійкості. За наявності кореня з нульовими дійсними частинами система буде нестійкою. Отже, для визначення стійкості системи необхідно розв’язати рівняння і визначити знаки дійсної частини коріння. Рівняння алгебри першого і другого ступеня розв'язуються просто. Рівняння вищих порядків розв'язуються важко або аналітично взагалі не розв'язуються. Тому виникає питання про визначення знаків коріння рівняння без розв’язку рівняння. Цим питанням займалися багато учених. Вони встановили непрямі ознаки, що дозволяють судити про знаки кореня. Ці непрямі ознаки одержали назву критеріїв стійкості.

Застосовуються критеріїв алгебри стійкості Вишнеградського, Рауса, Гурвіца і графоаналітичні критерії Михайлова і Найквіста. Перевагами критеріїв алгебри є простота їх застосування. Треба тільки знати розділ математики, що стосується розв’язування рівнянь. Основним недоліком критеріїв алгебри є те, що вони не дозволяють оцінити вплив на стійкість системи параметрів окремих її елементів. Від цього недоліку вільні графоаналітичні критерії.

1.7.2. Основні показники надійності автоматичної системи

Надійність – це властивість об'єкта (схеми) виконувати задані функції протягом часу, обумовлені вимогами експлуатації. Якщо на стадії проектування не врахувати надійність, то в реальних умовах розроблена схема керування може виявитись непрацездатною.

Питання надійності роботи окремих елементів регламентуються ГОСТ 27.002-83 "Надійність у техніці, терміни і визначення".

Основне поняття в теорії надійності Відмова – це (повна або часткова) втрата працездатності, порушення нормальної роботи об'єкта (схеми), внаслідок чого його характеристики не задовольняють вимог, які перед ним ставляться. Відмова завжди розглядається як функція неперервна в часі, вона може статись у будь-який момент часу і в той же час відмова – це дискретна величина. Розрізняють відмови трьох видів.

• технологічні (виникають за рахунок невідпрацьованої технології і незадовільного контролю якості в процесі виробництва);

• зношувальні (є наслідком старіння окремих елементів виробу);

• раптові (виникають випадково).

Розрізняють також Збій, який через деякий час ліквідується сам по собі. Збій призводить до короткочасного порушення працездатності виробу. Причина збою – неполадки в лінії зв'язку або енергопостачання.

Відповідно до ГОСТ 27.002-83 поняття надійність може включати: безвідмовність, довговічність, ремонтопридатність, збереженість.

Безвідмовність – властивість об'єкта безперервно зберігати працездатність протягом певного проміжку часу.

Довговічність – властивість об'єкта зберігати працездатність до настання граничного стану при існуючій системі технічного обслуговування.

Ремонтопридатність – пристосування виробу до попередження і виявлення причин виникнення його відмов, поломок і їх усунення шляхом проведення технічного обслуговування і ремонту.

Збереженість – властивість виробу бути справним і працездатним під час зберігання, транспортування і після них.

Використовуються поняття, які характеризують властивості об'єкта (схеми) це: справний і несправний, працездатний і непрацездатний.

Справний стан – це стан, при якому виріб відповідає всім вимогам, що встановлені нормативно-технічною документацією.

Несправний – стан коли виріб не відповідає хоча б одній із вимог.

Працездатний і Непрацездатний стан характеризується здатністю і нездатністю виробу виконувати задані функції з збереженням значень, параметрів відповідно до нормативно-технічної документації.

Граничний стан – такий, при якому наступна експлуатація повинна бути припинена через неможливість ліквідувати порушення вимог правил техніки безпеки, відхилення параметрів від норми, а також через необхідність проведення капітального ремонту.

Пошкодження – явище, яке полягає в порушенні справності виробу під дією зовнішніх факторів, які перевищують норми, встановлені в нормативно-технічній документації.

До кількісних показників надійності відносяться: ймовірність безвідмовної роботи, інтенсивність відмов, напрацювання на відмову, середній термін служби, середній термін зберігання та ін.

Таблиця1.20 Час експлуатації для визначення імовірності

безвідмовної роботи

Перелік установок	Час, годин
Установки, які працюють постійно ( мікроклімат, водопостачання...).	4000
Установки мікроклімату сезонного призначення	1000
Установки для приготування і роздачі кормів, видалення гною, доїння і обробки молока,...	500
Установки для обробки зерна	400

Ймовірність безвідмовної роботи Р(t) – ймовірність того, що в заданому інтервалі часу при заданих режимах і умовах роботи не виникне відмова виробу в роботі:

Р(t) =

K – коефійціент, що враховує вплив навколишнього середовища на роботу електрообладнання та засоби автоматизації, для с. г. виробництва k=10;

λΣ – загальна інтенсивність відмов, год-1;

То – час експлуатації, для якого визначається імовірність безвідмовної роботи, знаходимо по таблиці 1.20.

Таблиця 1.21 Інтенсивність відмов

Назва електрообладнання	Інтенсивність Відмов 1х 10-6 год-	Назва електрообладнання	Інтенсивність відмов, 1х 10-6 год-1
1	2	3	4
Автоматичний вимикач Випрямляч Вимикач кнопковий Вимикач панельний Вимикач кінцевий Перемикач триполюсний Виконуючий механізм Датчики контактні температури Датчики контактні рівня Датчики контактні тиску Датчики контактні вологості Діоди, фото датчики Дзвінок, Електродвигуни Елемент нагрівний Електроклапан Електричний регулятор рівня Запобіжник Затискач запобіжника Заглибний електродвигун Заслінка Кнопки керування Конденсатори паперові Конденсатори керамічні Контакти замикаючі Контакти розмикаючі Лампочки сигнальні Лампи розжарювання Лампове штирове з’єднання Логічні елементи Логометри, мілівольтметри Контакти Показові прилади Підсилювач постійного струму Потенціометр дротяний Потенціометр Магнітні пускачі Манометр з трубчастою пружиною	0,22 1,00 0,063 0,175 0,161 0,92 110 4,5 1,5 5,0 1,5 1,5 16 10 0,3 25 42 0,6 0,02 25 2,9 1,4 1,8 0,1 0,25 0,25 20,0 0,625 0,005 2,5 380 0,25 38 10 1,4 105 10 100	Мікроконтролер Мікровимикачі Регулятор тиску РД-8 Резистори пластині Резистори потужні Резистори дротяні Резистори шунтуючі Реле потужні Реле теплові Реле загального призначення Реле часу електронне Реле часу електромеханічне Реле часу електромагнітне Рубильник Регулятор тиску Регулятор електронний рівня Регулюючі електричні прилади Серводвигун Сирена Тиристор Транзистор кремнієвий Транзистор германієвий Трансформатор Тахогенератор Термореле Терморезистор Терморегулятор електронний Терморегулятор електромеханічний Тензодатчики Тепловий вимикач УВТЗ без позисторів ЗОУП – 25 Інтегральні схеми Тумблер Тахометр електричний З’єднання пайкою, затискачі Тиратрон Лампа імпульсна	40 0,25 26 0,03 0,025 0,068 1,5 0,30 0,40 0,25 1,2 2,5 0,5 6,6 25 2,5 60 0,25 20 1,8 0,5 0,3 5 0,8 0,14 3,8 23 36 10 0,1315 24 22 0,1 0,52 11,5 0,04 0,2 0,9

Інтенсивність відмов для кожного виду елементів вибираємо з таблиці 1.21

Інтенсивність відмов установки залежить від дії механічних впливів на електрообладнання і від розміщення кожного елемента схеми. Коефіцієнт який враховує механічні впливи вибираємо з таблиці 1.22.

Таблиця 1.22 Значення коефіцієнта навантаження від умов експлуатації

Умови експлуатації	Коефіцієнт
Лабораторні Стаціонарні Транспортні Польові	1,00 1,07 1,46 1,54

На інтенсивність відмов також впливає температура та вологість оточуючого середовища при яких працює елемент схеми або установка в цілому. Коефіцієнт температури, який залежить від вологості і температури при яких працюють елементи схеми вибирають з таблиці 1.23.

Таблиця 1.23 Значення коефіцієнта температури від температури і вологості середовища

Вологість	Температура	Коефіцієнт	Вологість	Температура	Коефіцієнт
60...70	20...40	1,0	90...98	20...25	2,0
70...80	20...30	1,25	90...98	25...30	2,2
70...80	30...40	1,45	90...98	30...40	2,5
80...90	20...30	1,4	90...98	40...100	3,4
80...90	30...40	1,8	90...98	100 і більше	4,0

Інтенсивність відмов для кожного виду елементів визначаємо по формулі враховуючи коефіцієнт навантаження та температури, при яких дане електрообладнання використовується

λ=k λо ;

Де λо – інтенсивність відмов в нормальних умовах, год.-1 (таблиця1.21);

k – поправочний коефіцієнт, який враховує коефіцієнт навантаження і температури;

К = kН kТ,

Де kН – коефіцієнт навантаження, який залежить від умов при яких працює елемент схеми, вибираємо з таблиці 1.22;

KТ – коефіцієнт температури, який залежить від температури і вологості в яких знаходиться елемент схеми, вибираємо з таблиці 1.23.

Всі дані заносимо до таблиці 1.24.

Таблиця 1,24 Зразок таблиці для розрахунку інтенсивності відмов

Назва Елемента	Позначення	Кількість	Інтенсивність відмов 10-6 Год.-1	Коефіцієнт Навантаження Кн	Режим роботи	Поправочний коефіцієнт, к	Інтенсивність Відмов 10-6год.-1
Температура, ОС	Коефіцієнт Температури, Кт	Для одного елемента	Для групи елементів
Вимикач автоматичний	QF	1	0,22	1.07	20	1,4	1,49	0,33	0,33

Ймовірність відмови – величина за значенням протилежна Р(t). При цьому: Р (t) + q (t) = 1, звідки q (t) = 1 - Р (t).

Напрацювання на відмову – величина обернена сумарній інтенсивності відмов

Т =1/ λΣ

Напрацювання на відмову з заданою імовірністю визначаємо по формулі:

То = ℓn(р)/λΣ ;

Для підвищення надійності установки потрібно зробити резерв малонадійного обладнання в необхідній кількості для того, щоб установка працювала задану кількість часу.

• < Назад
• Вперёд >