Методистские указания по курсу коллоидной химии
Страница 1 из 2
Методистские указания по курсу коллоидной химии
Обучающие задания по курсу коллоидной химии для студентов 3 курса технологического факультета
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
*** Мера раздробленности вещества или степень дисперсности: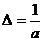 , м3,
, м3,
Где А – размер частицы: d - диаметр для шарообразной, l - ребро куба для кубической.
*** Удельная поверхность S(уд.) = S/V ≈ S/V, м3,
Где S и V– суммарные поверхность и объем дисперсной фазы; s и v - поверхность и объем одной частицы.
*** Число коллоидных частиц в заданном объеме золя:
ν = M (вещества)/ m(коллоидной частицы).
*** Количество вещества коллоидных частиц: Nd = ν/NA.
*** Частичная молярная концентрация (молярность) золя: Cd = Nd / V(золя).
*** Средняя молярная масса коллоидной частицы:
Md = M(коллоидной частицы) × NA, г/ моль
ОСНОВНЫЕ КОНСТАНТЫ
Постоянная Авогадро NA = 6,02× 1023 моль-1
Универсальная газовая постоянная R = 8,314 Дж/ К моль = 62,36 л(мм рт. ст.)/К моль
1 а. е.м. = 1,66 ×10-24 г
Постоянная Больцмана K = R/ NA = 1,38×10-23 Дж/К
Диффузия – самопроизвольный процесс выравнивания концентрации по всему объему раствора за счет броуновского движения.
Уравнение Эйнштейна позволяет связать коэффициент диффузии D с величиной среднего сдвига:
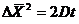 (1)
(1)
Уравнение Эйнштейна – Смолуховского связывает величину среднего сдвига с вязкостью η и формой частиц:
 (2)
(2)
Объединив уравнения (1) и (2), для частиц сферической формы получим:
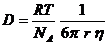 (3)
(3)
Пример 1. Оцените коэффициент диффузии сферической частицы радиусом 1,5 ×10-9 м в воде при 300оК.
Решение.
Воспользуемся уравнение (3). R/ NA = k – постоянная Больцмана; η(Н2О) = 1 ×10-3 Н с/м2.

Пользуясь уравнением (3) можно экспериментально определить радиус частицы по известным значениям вязкости и коэффициента диффузии.
Седиментационно – диффузионное равновесие коллоидных частиц
Для шарообразных частиц с радиусом r при их падении в жидкости с вязкостью η
Сила трения рассчитывается по формуле:
F = 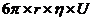 (4),
(4),
Где U –скорость оседания частицы.