МЕТОДИЧЕСКИЕ УКАЗАНИЯ По выполнению лабораторно-практических занятий и заданий для самостоятельных работ по дисциплине «Физическая и коллоидная химия»
Страница 10 из 11
3.4.1. Какими свойствами обладает жидкость в слоях, расположенных у границы раздела фаз с твердым телом?
3.4.2. Как влияет на адсорбцию природа адсорбента, адсорбтива и растворителя?
3.4.3. Как изменяется структура жидкости в граничных слоях по сравнению со структурой в объеме?
3.4.4. С чем связана сложность математического описания процесса молекулярной адсорбции из растворов?
3.4.5. Каковы особенности применения правила Траубе – Дюкло для молекулярной адсорбции дифильных ПАВ из растворов?
3.4.6. В чем заключается правило уравнивания полярностей Ребиндера? Приведите конкретные примеры.
3.4.7. Какой вид имеют изотермы адсорбции растворенных веществ на поверхности твердых тел?
3.4.8. Какие уравнения применяются для математического описания концентрационной зависимости адсорбции на границе раствор – твердое тело?
3.4.9. Каков физический смысл констант уравнения Ленгмюра?
3.5. Задачи для самостоятельного решения
3.5.1. По уравнению Фрейндлиха – Бедекера вычислите равновесную концентрацию уксусной кислоты, если известно, что 1 г угля адсорбирует 3,76 ммоль кислоты. К = 2,82, n = 2,44.
3.5.2. . По результатам эксперимента постройте изотерму адсорбции. Определите вид уравнения Фрейндлиха – Бедекера, найдя графически константы уравнения:
А) адсорбируемое вещество – ацетон, адсорбент – активированный уголь
|
С, моль/л
|
2,34
|
14,65
|
88,62
|
177,69
|
268,97
|
|
Г, моль/г
|
0,208
|
0,618
|
1,500
|
2,080
|
2,880
|
Б) адсорбируемое вещество – уксусная кислота, адсорбент – кровяной уголь
|
С, моль/л
|
0,018
|
0,031
|
0,062
|
0,126
|
|
Г, моль/г
|
0,467
|
0,624
|
0,801
|
1,440
|
В) адсорбируемое вещество – уксусная кислота, адсорбент – кровяной уголь
|
С, моль/л
|
0,268
|
0,471
|
0,882
|
|
Г, моль/г
|
1,55
|
2,04
|
2,48
|
3.5.3. Поверхность 1г активного древесного угля 1000 м2. Сколько литров аммиака при стандартных условиях может адсорбироваться на поверхности 45 г угля, если вся поверхность полностью покрыта. Диаметр молекулы метана 3 10-8 см.
3.5.4. Получены следующие данные по адсорбции на древесном угле уксусной кислоты из водных растворов. (Во всех случаях объем раствора 200 мл):
|
Начальная концентрация со, моль/л
|
Равновесная концентрация, с, моль/л
|
Масса угля, m, г
|
|
0,503
|
0,434
|
3,96
|
|
0,252
|
0,202
|
3,94
|
|
0,126
|
0,0899
|
4,00
|
|
0,0628
|
0,0347
|
4,12
|
|
0,0314
|
0,0113
|
4,04
|
|
0,0157
|
0,00333
|
4,00
|
Покажите, что эти данные удовлетворяют изотерме адсорбции Фрейндлиха. Оцените константы уравнения.
3.5.5. * Равновесие адсорбции молекул уксусной кислоты (НА) на активированном угле из растворов в неводном неполярном растворителе описывает уравнение Ленгмюра:
Г = 
, где НА– молекула кислоты в растворе; 
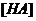– равновесная концентрация НА в растворе, моль/л; 
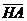- молекула НА на поверхности активированного угля; 
- концентрация адсорбированной кислоты НА, моль/г; t – максимальная емкость сорбента по отношению к НА; (t = 5 10-4 моль/г) ; К – константа сорбционного равновесия, л/моль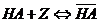 
, где Ц – сорбционный центр активированного угля, не занятый молекулой НА.
При некоторой температуре для адсорбции НА из раствора объемом 100 мл на образце сорбента 1 г получены следующие данные:
|
Исходные концентрации НА (С), моль/л
|
|
10-4*
|
2,5 10-4*
|
5 10-4*
|
10-3
|
5 10-3
|
10-2
|
5 10-2
|
|
Гэксперим.
|
1,66 10-2
|
4,15 10-2
|
8,2 10-2
|
0,16
|
0,60
|
0,78
|
0,925
|
|
Грасчет.
|
|
|
|
|
|
|
|
1) определите константу К, пользуясь данными таблицы, отмеченными *.
2) Считая, что в системе раствор – сорбент устанавливается единственное равновесие (сорбция – десорбция) и, пользуясь уравнением Ленгмюра, заполните пропуски в таблице.
3) Объясните полученные результаты. Ответ подтвердите расчетом.
4) Предложите независимый экспериментальный метод, применение которого может подтвердить Ваш ответ на вопрос 3.
