МЕТОДИЧНІ ВКАЗІВКИ З ВИКОНАННЯ КУРСОВОЇ ТА ДИПЛОМНОЇ РОБІТ

Другим параметром, що характеризує сукупність, є Середнє квадратичне відхилення. Цей показник має виключне значення в математичній статистиці. Він використовується як абсолютна міра різноманітності і, до того ж, його покладено в основу майже всіх характеристик мінливості, розподілу, кореляції, регресії, дисперсійного тощо.

Oсновна формула, за якою визначається середнє квадратичне відхилення:

,

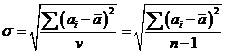Де 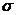(сигма) - середнє квадратичне відхилення (назва цього символу перейшла й на сам показник - середнє квадратичне відхилення часто називають просто сигмою); (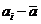) - центральне відхилення, тобто різниця між кожною варіансою і середньою арифметичною; V - число степенів свободи; при розрахунках сигми число степенів свободи дорівнює кількості варіанс без одної, тобто V=п - 1.

Це пояснюється тим, що при обчисленні сигми є одне обмеження величини ознаки у об'єктів, що вивчаються. Сигма вираховується для певної групи, яка має певну середню арифметичну. Тому різноманітність елементів, що утворюють середнє квадратичне відхилення, обмежена цією однією умовою, отже, число степенів свободи буде дорівнювати кількості варіанс без одної.

Сигму майже ніколи не обчислюють за наведеною вище формулою, це дуже незручно, адже треба спочатку обрахувати середню арифметичну і лише згодом - сигму. Тому було запропоновано низку інших формул, які значно спрощують обрахунки.

Ось одна з них, дуже зручна при обрахунках на ЕОМ:

1.4.3.4. Параметри об'єднаної вибірки

Інколи виникає потреба обрахувати середню арифметичну та сигму для узагальненого розподілу, тобто коли декілька виборок об'єднуються в одну. При цьому, як правило, вихідні розподіли не відомі, а наводяться лише їхні середні та сигми. Це часто трапляється, коли доводиться аналізувати дані інших авторів. У таких випадках середня та сигма визначаються за наступними формулами:

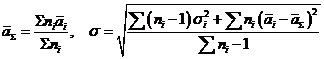
Де ni - чисельність окремих груп, включених до узагальненого розподілу; 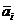- середня арифметична кожної з цих груп; 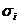- сигма кожної окремої групи; 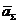- середня арифметична узагальненої вибірки.

Тепер, коли вже відомо, що таке сигма, саме час повернутись до властивостей нормального розподілу (див. рис. 4). Отже, однією з найголовніших властивостей є те, що 68,268 % усіх варіанс міститься в межах від ( ) до (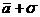), 95,45 % - від () до ( ) (тобто лише 4,6 % дат виходить за межі цього інтервалу), 99,73 % - від () до ( ) (за межі цього інтервалу виходить лише 0,3 % дат). Поза межами інтервалу лишається зовсім незначна кількість дат (0,006 %).

1.4.3.5. Коефіцієнт варіації

Середнє квадратичне відхилення є основним показником різноманітності варіанс, об'єднаних до вивчених виборок. Проте сигма може вважатись безпосереднім показником варіювання лише при виконанні наступних умов:

1) порівнюються лише тотожні за розмірністю ознаки меристичні, вагові тощо;

2) середні арифметичні порівнюваних виборок не дуже різняться між собою.

Якщо вказані умови не витримуються і необхідно порівнювати різноманітність різних ознак або тотожних ознак при значній різниці між середніми, сигма не може використовуватись для порівняння варіювання ознак у вибірках. Тому застосовується особливий показник — коефіцієнт варіації (СV). Цей показник є функцією обох основних параметрів вибірки – середньої арифметичної (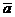) та середнього квадратичного відхилення (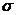), є безрозмірною величиною, а тому дуже зручний для порівняння варіювання будь-яких ознак. Обчислюють коефіцієнт варіації за наступною формулою:

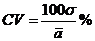
1.4.3.6. Похибка середньої арифметичної

Існує ще одна характеристика будь-якої сукупності – Похибка середньої арифметичної. Зрозуміло, що те, наскільки правильно середня арифметична вибірки буде відображати середню характеристику генеральної сукупності, залежить від двох величин: від ступеня варіювання тієї чи іншої ознаки в генеральній сукупності та від чисельності вибірки. Останнє легко зрозуміти, бо чим більша чисельність вибірки, тим більша частина генеральної сукупності досліджується, отже, з тим меншою помилкою буде зроблено висновок щодо середньої для всієї генеральної сукупності.

З іншого боку, чим більше варіювання ознаки, тим вона мінливіша, тим більша ймовірність потрапити на таку вибірку, середня буде дуже відрізнятись від генеральної середньої. Отже, чим більша різноманітність (яка вимірюється сигмою), тим більша похибка репрезентативності.

Виходячи з вищенаведеного, похибка середньої арифметичної оцінюється за формулою:

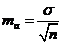
У тих рідкісних випадках, коли до вибірки потрапляє понад 30-50 % варіанс генеральної сукупності, вказаний показник домножується на 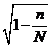, тобто формула набуває вигляду:

.

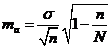Не варто плутати статистичну похибку з методичними помилками та помилками точності (точність вимірювань, аналізів, розрахунків тощо). У даному випадку йдеться про величину розходження між значеннями вивчених ознак у виборці та в генеральній сукупності. Чим краще взято вибірку, чим більші її розміри, тобто чим вірніше вона репрезентує генеральну сукупність (увесь процес, явище), тим меншою є статистична похибка і розходження між значеннями ознак у вибірковій та генеральній сукупностях. Незважаючи на неминучість статистичної похибки, її можна звести до мінімуму, взявши вибірку з достатньою кількістю варіанс. Таким чином, статистична похибка дозволяє робити висновок щодо надійності, або вірогідності одержаних результатів, тобто відносно того, чи досить було зроблено вимірювань, щоб при даній величині мінливості можна було б за вибіркою характеризувати цілісність.